Network meta-analysis

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

Age-related macular degeneration: diagnosis and management. London: National Institute for Health and Care Excellence (NICE); 2018 Jan. (NICE Guideline, No. 82.)

Cover of Age-related macular degeneration

Age-related macular degeneration: diagnosis and management.

Show details

Contents

< Prev Next >

Appendix GNetwork meta-analysis

G.1. Methods

G.1.1. General

All NMAs followed the generalised linear modelling framework recommended by the NICE Decision Support Unit (see Technical Support Document 2 [Dias et al. 2011a]).

The choice of reference comparator – that is, the treatment with which all other treatments are compared – within a network meta-analysis is mathematically arbitrary (DSU TSD2 [Dias et al. 2011a]); however, computational efficiency is improved by selecting an option that is ‘well connected’ in the network, with a good amount of data available. For this reason, the reference treatment for all NMAs was ranibizumab 0.5 mg 1-monthly.

G.1.1.1. Basic model specification

Particular models fitted for specific datatypes are detailed below. However, all models shared the same basic structure:

Fixed- and random-effects models were explored for relative treatment effects.

In the fixed-effect model, a common effect is assumed for treatments across all trials and, for all j>1, the relative effect (δ) of the treatment (t) in arm j of trial i compared with the treatment in arm 1 of trial i is estimated as the difference between the comparators in each pair:
$δ_{i, j} = d_{t_{i j}} - d_{t_{i 1}},$
(1)
with the ds representing the effect of each treatment relative to the ‘reference’ option in the network – so, in the case of t_i1=1 (that is, the treatment in arm 1 of trial i is ranibizumab 0.5 mg 1-monthly), d_{t_i1}=0.
In the random-effects model, trial-specific estimates of relative effect between each treatment and the treatment in arm 1 are assumed to be exchangeable and drawn from a shared distribution. In this implementation, normal distributions of treatment effects are assumed, the mean (d_{t_ij} − d_{t_i1}) is specific to each pairwise comparison of interest and the variance (σ²) is assumed to be common to all comparisons. That is,
$δ_{i, j} ~ N (d_{t_{i j}} - d_{t_{i 1}}, σ^{2}) .$
(2)

Trial-specific ‘baselines’, μ_i, are estimated as unrelated nuisance parameters, and combined with relative effects so that the observed data (as transformed through an appropriate link function; see below) in arm j of trial i (θ_ij) can be seen as a linear combination of these parameters:

θ_{i j} = μ_{i} + δ_{i, j} .

(3)

G.1.1.2. Meta-regression

Every treatment in every trial could be viewed as a combination of 3 factors: agent, dose and treatment regimen. For all outcomes, models were explored that treated each treatment option in the network as a discrete, mutually exclusive combination of these 3 things (for example, bevacizumab 1.25 mg monthly -v- ranibizumab 0.5 mg monthly -v- ranibizumab 0.5mg PRN… and so on).

However, because there are shared features between the treatment regimens, we also explored models in which identical intra-agent features of regimens were assumed to result in identical effect modification across all agents, using a meta-regression approach (see NICE Decision Support Unit Technical Support Document 3 [Dias et al. 2011b]). For example, we fitted models in which the difference between PRN treatment and routine monthly treatment was assumed to be the same for all agents. In this formulation, model (3) is extended such that observed treatment effects are modelled as a combination of baseline, agent-level treatment effect and effect of PRN administration:

θ_{i j} = μ_{i} + δ_{i, j} + β (x_{i, j} - x_{i, 1}),

(4)

Where β is the effect of PRN administration and x_i,j and x_i,1 are dummy variables indicating whether a PRN strategy was used in arm j and arm 1, respectively, of trial i. Clearly, in any contrast for which both or neither arm have a PRN regimen, this term reduces to 0.

This framework could be extended to include as many covariates as the data will support. We explored the impact that was made by including the following in this meta-regression approach:

Table 1Potential meta-regression covariates

Covariate	Definition
PRN	PRN (treatment as needed) compared with a routine monthly schedule. Note that this covariate applies to anti-VEGF strategies, only; all PDT regimens were given on a PRN basis, but were coded as 0 as there was no opportunity to differentiate between routine and PRN regimens (and, were evidence available, the degree of effect modification could easily be quite different). As a matter of principle, we would have been interested in exploring whether PRN regimens with different follow-up times have different results. However, no evidence was included that allowed us to test this, as all PRN regimens had similar follow-up frequencies (all were essentially monthly).
Loading	Supplementing a PRN schedule with an initial loading phase (invariably monthly injections in months 0, 1 and 2). Note that this covariate applies to PRN schedules only. Analogous loading phases were included in some of the RCTs exploring routine injections at greater than monthly intervals, and an attempt was made to model these separately; however, in that instance, there were insufficient data to be able to distinguish effects. For this reason, e.g., 3-monthly regimens with an initial loading phase are coded 0 for this covariate.
TREX	Treat-and-extend regimen compared with a routine monthly schedule.
PRNX	PRN-and-extend regimen compared with a routine monthly schedule. This appears in only 1 RCT (SALUTE 2015), in which the strategy (referred to as ‘wait and extend’) is compared with a conventional PRN approach (both using ranibizumab 05.mg). Because there is only 1 datapoint, there is no material difference between including the arm as a separate node within the network and coding it as PRN with a covariate for PRNX. The latter approach has the small advantage that the estimated effect the PRNX regimen makes can be directly seen rather than inferred from the difference between 2 nodes. In turn, this makes it easier to explore what the impact of such a regimen might be on agents other than ranibizumab.
Frequency (interval between injections in months)	For 1 or more anti-VEGF agent, evidence was available on routine 1-monthly, 6-weekly, 2-monthly and/or 3-monthly administration frequencies. These were coded as 1, 1.5, 2 and 3, respectively, to provide a continuous estimate of effect modification for every month between injections over and above 1. The guideline committee suggested that there was a priori reason to imagine that frequency–response effects might plausibly be different between different anti-VEGF agents. Therefore, 3 different approaches to modelling frequency were explored. In model a, a single coefficient – assumed to be shared between all agents – was estimated. In model b, separate coefficients were estimated for each agent. In model c, 2 coefficients were used – 1 shared between bevacizumab and ranibizumab (which are pharmacologically very closely related) and a separate term for aflibercept. A fourth approach might be proposed, in which each treatment’s effect is modelled as belonging to a shared distribution; however, large quantities of data are typically required in order to estimate such a model or, alternatively, an informative prior has to specified to limit the spread of the distribution to a plausible degree (and, in this relatively abstract case, it would have been difficult to elicit meaningful values for this even from the experienced members of the guideline committee). Once more, this covariate only applied to anti-VEGF treatments. Although all PDT regimens were provided on a 3-monthly (PRN) basis, they were coded as monthly for the purposes of these models, so that the effect of PDT-3-monthly-PRN, as a standalone node, would not influence estimation of frequency–response gradients for anti-VEGFs.

Because there was relatively little variety in the doses used in trials, and it was not deemed appropriate to assume that effect modification would be the same across agents on a milligram-for-milligram scale, a similar approach was not explored for dose–response effects. Therefore, we retained each agent–dose dyad as discrete nodes within the network in all analyses. There was one exception to this rule: on the advice of the guideline committee, we assumed 0.3 mg and 0.5 mg doses of ranibizumab were interchangeable, and combined them into a single node. We tested this in a sensitivity analysis, which confirmed that model fit was not improved by treating these doses as separate, with the addition of extra nodes leading to inferior DIC; therefore, the committee’s expectation was validated.

G.1.1.3. Prior distributions

Non-informative prior distributions were used in all models.

Trial baselines and treatment effects were assigned N(0, 100²) priors.
The between-trial standard deviations used in random-effects models were dependent on the datatype:
- U(0, 50) for continuous BCVA data (natural scale)
- U(0, 10) for categorical BCVA data (probit scale)
- U(0, 5) for dichotomous discontinuation data (log-odds scale)
In categorical models
- inter-category intervals were given U(0, 5) priors.
- inter-trial random-effects for inter-category intervals were given U(0, 2) priors.
In meta-regression models, all covariates were assigned N(0, 1000) priors.

G.1.1.4. Model selection

Model selection was performed on the basis of multiple discriminatory variables.

Deviance information criterion (DIC; Spiegelhalter et al. 2002): an estimate of deviance that is ‘penalised’ according to the number of parameters in the model (adding parameters to a model should increase its ability to predict known data; however, this may come at the expense of reducing its ability to predict external datasets). A difference of least 3 points in DIC is commonly used to define meaningfully different models; we did not use this as an absolute arbiter of superior fit, though it was still important to define clearly different models.
Total residual deviance: a calculation of the model’s ability to predict the individual datapoints underlying it. In every iteration of the model sampling procedure, the amount each model-estimated datapoint deviates from the observed evidence is calculated, summed and averaged over all iterations. Each datapoint is expected to contribute approximately 1 to the posterior mean deviance; therefore, the total residual deviance of a well-fitting model will be approximately the same as the number of independent datapoints in the model (DSU TSD2 [Dias et al. 2011a]).
SD of random-effects term (tau): where a random-effects model is fitted, the width of the inter-study heterogeneity distribution estimated by the model is a reflection of heterogeneity in the underlying data. Therefore, while not a measure of goodness of fit per se, it is useful to consider as an indication of how broad a model is required to fit the data. For example, if the introduction of a covariate results in a smaller inter-study random-effects, term, it can be inferred that a propotion of inter-study heterogeneity has been explained by the new term. Because inter-study heterogeneity is not modelled in fixed-effects models (that is, tau is assumed to be 0), there is no analogous quantity that can be used to compare different fixed-effects models.

Particular attention was paid to model selection for the most critical synthesis for the health economic model – bivariate normal WMD at 12 and 24 months (see G.2.1.1.1.1). Once an optimal model had been selected for this outcome, we took the view that it would be helpful (and convenient for parameterising our HE model) to adopt a consistent specification for all other models, provided it did not result in conspicuously worse fit than was available with another choice. Therefore, we examined model fit statistics, in these other cases, with a view to establishing whether it was clearly incorrect to support the globally preferred model, rather than re-establishing whether that model should be preferred.

G.1.1.5. Baseline syntheses

While NMAs provide a coherent estimate of relative effect, it is often necessary to combine these with an estimate of absolute effect in order to estimate expected outcomes of treatment (most importantly, in the present context, in order to deploy outputs in a health economic analysis). Put more simply, the NMAs tell us how much more or less likely people are to experience the event of interest, given the treatment to which they have been assigned, but additional evidence is necessary to estimate ‘more likely than what?’

To do this, we synthesised arm-level data from included RCTs, following the recommendations of NICE DSU TSD5 (Dias et al. 2011c). Data from trials reporting the effect of ranibizumab 0.5 mg monthly were pooled using the same Bayesian generalised linear modelling framework that was used in the NMAs of treatment effect. Likelihoods and link functions were as specified for the datatypes below. Prior distributions were identical to those used in NMAs (see G.1.1.3). OpenBUGS code is provided in G.4.2.

G.1.1.6. Computation

Models were run in OpenBUGS 3.2.2. Code for all selected models in provided in G.4.

Results were reported summarising 10,000 samples from the posterior distribution of each model, having first run and discarded 50,000 ‘burn-in’ iterations. Three separate chains with different initial values were used.

Outputs from the chains, including autocorrelation plots, were visually inspected to assess convergence. In some instances, it was necessary to introduce additional burn-in samples and/or ‘thin’ posterior samples (e.g. by taking 1 in every 100 sampled values). In every case, it was possible to produce well converged results in this way.

G.1.2. Continuous variables

The only continuous outcome of interest was absolute BCVA, for which mean change from baseline to follow-up was the point of synthesis.

It is common, in such circumstances, to fit identity-link models, which rely on a normal likelihood (see NICE DSU TSD2 [Dias et al. 2011a]). Although we assume, elsewhere in the analysis undertaken for this guideline, that mean change in BCVA is likely to be normally distributed, the synthesis model adopted here does not rely on this assumption; rather, it assumes that the sample means are normally distributed (given sufficiently large samples, this would be expected to be the case regardless of skewness in the underlying data, according to the Central Limit Theorem).

However, in this case, we have reasonable amounts of 1-year and 2-year follow-up data, which can be expected to be correlated. For that reason, we concluded it was superior to perform synthesis in a single analysis, extending the simple continuous model to the bivariate case, and estimating effects – and effect modifiers – for both timepoints at the same time.

We are interested in estimating outcomes for time interval (0,1) and time interval (0,2). The outcomes for interval (1,2) will also be of interest, especially for deployment in the health economic analysis; however, this can be trivially inferred by deducting (0,1) from (0,2).

When the data are assembled, we have 2 distinct situations that need to be accounted for in the same model.

1-year RCTs provide data on interval (0,1) only. Extending the notation of equations (1) and (2) to encompass time-intervals, we have

δ_{i, j, (0, 1)} = d_{t_{i j \cdot} (0, 1)} - d_{t_{i_{1}}, (0, 1)},

(5)

for the fixed-effects implementation. For the random-effects version, interval-specific inter-study heterogeneity is modelled:

δ_{i, j, (0, 1)} ~ N (d_{t_{i j}, (0, 1)} - d_{t_{i_{1}}, (0, 1)}, σ_{(0, 1)}^{2}) .

(6)

An approach with a shared variance term for intervals (0,1) and (1,2) was explored, but provided clearly inferior model fit than allowing separate variance terms in each interval.

2-year RCTs provide data on (0,1) and (0,2) and require a multivariate likelihood. Let m_i,j,(0,1) be the mean change for (0,1), with standard error se_i,j,(0,1). Similarly, let m_i,j,(0,2) be the mean change for (0,2), with standard error se_i,j,(0,2). Then the joint likelihood (Franchini et al. 2012) is:

(\begin{matrix} m_{i, j, (0, 1)} \\ m_{i, j, (0, 2)} \end{matrix}) ~ N ((\begin{matrix} θ_{i, j, (0, 1)} \\ θ_{i, j, (0, 2)} \end{matrix}), (\begin{matrix} s e_{i, j, (0, 1)}^{2} & s e_{i, j, (0, 1)}^{2}) \\ s e_{i, j, (0, 1)}^{2} & s e_{i, j, (0, 2)}^{2} \end{matrix})),

(7)

with θ_i,j,(0,1) and θ_i,j,(0,2) defined with interval-specific baselines and effects as per (3) (or (4) in the case of a meta-regression model).

The model for δ_i,j,(0,1) is as per (5) and (6) for interval (0,1). For the interval (0,2), it is the sum of the (0,1) effect and a new term for the (1,2) change. That is,

δ_{i, j, (0, 2)} = δ_{i, j, (0, 1)} + δ_{i, j, (1, 2)},

(8)

with δ_i,j,(1,2) defined as the study-specific treatment effect over interval (1,2). In a fixed-effect model, this is

δ_{i, j, (1, 2)} = d_{t_{i j}, (1, 2)} - d_{t_{i 1}, (1, 2)}

(9)

and, in the random-effects version, it becomes

δ_{i, j, (1, 2)} ~ N (d_{t_{i j, (1, 2)}} - d_{t_{i_{1}}, (1, 2)}, σ_{(1, 2)}^{2}) .

(10)

Treatment effect estimates on interval (0,2) can be derived as

d_{k, (0, 2)} = d_{k, (0, 1)} + d_{k, (1, 2)} .

(11)

In theory, it would be possible for 2-year RCTs to provide data on only (0,2) or on (1,2) and (0,2). These could easily be integrated in this model. In practice, there were no such trials in our evidence-base.

G.1.2.1. Weighted mean differences and standardised mean differences

Differences between continuous treatment effects – in this case, differences in change from baseline to follow-up – can be expressed on the natural scale on which they have been estimated – in this case, ETDRS letters – in the form of a weighted mean difference.

However, it may also be useful to standardise the contrasts by scaling each by a common standard deviation, so that each RCT provides data on how many SDs difference is observed between treatments. In the case in hand, there was particular value in doing this, as it provided convenient outputs for the health economic analysis.

Whereas, in a pairwise analysis, it is conventional to scale the pairwise difference by the pooled SD of the 2 observations, this can be extended, in the context of NMA, so that all trial-level contrasts are scaled by a SD pooled across all arms of a trial. So, for each of a arms of trial i at timepoint y, with observed SDs si,j,y, the pooled estimate is

s_{i, y} = \sqrt{\frac{\sum_{j = 1}^{j = a_{i}} s_{i, j, y}^{2} (n_{i, j, y} - 1)}{\sum_{j = 1}^{j = a_{i}} (n_{i, j, y} - 1)}}

(12)

This quantity is then used to scale the linear predictors, so that

θ_{i, j, y} = (μ_{i, y} + δ_{i, j, y}) s_{i, y} .

(13)

Meta-regression terms may be incorporated into the linear predictor to be scaled, as per (4).

G.1.2.2. Imputing missing SDs

As is common in syntheses of continuous measures of change, a nontrivial proportion of RCTs did not provide a direct estimate of variability.

Where SEs or confidence intervals were available, these were converted into SDs.

In 1 case (TREX), a change value and its dispersion was not reported, but estimates of baseline and follow-up BCVA along with SDs were available. In this circumstance, the mean change is trivially calculated as BCVA_endpoint – BCVA_baseline; however, in order to estimate the variance of the change, it is necessary to specify a coefficient representing within-patient correlation between baseline and follow-up. In the absence of other data, we assumed a correlation coefficient of 0.5, which is commonly adopted in this circumstance and is considered conservative (NICE DSU TSD2 [Dias et al., 2012]).

In cases in which no estimate of dispersion was provided, but categorical counts of people achieving different levels of gain/loss were available, the missing continuous variance (σ²) of arm k of trial j could be approximated by

σ_{j, k}^{2} = \frac{\sum_{i = 1}^{i = c_{j, k}} n_{i, j, k} {(x_{i} - M C_{j, k})}^{2}}{\sum_{i = 1}^{i = c_{j, k}} n_{i, j, k}},

(14)

, where c_j,k is the number of categories reported in the arm, x_i is the average value for the category in question (mostly defined as the midpoint of the range; see below), n_i,j,k is the number of people achieving that level of change and MC_j,k is the reported mean change.

Where possible, we defined the average value for each category (x_i) as the midpoint of the range of changes (e.g. −29 to −15 letters = −22 letters). However, this was not possible for ‘open-ended’ categories (e.g. ≥30 letters gained), which exist in all cases. For these, we assumed that the unknown value for all open intervals was constantly proportional to the upper (or lower) bound, and used numerical optimisation (Microsoft Excel’s solver add-in) to estimate the optimal value of the multipliers by minimising RMSE across all cases where a categorically estimated SD could be compared with a true, reported SD. This predicted that the mean value of ‘left-unbounded’ intervals was 1.65 times its upper bound (e.g., for ≤−15, −15×1.65=−24.7) and the mean value of ‘right-unbounded’ intervals is 1.56 times its lower bound (e.g., for ≥+15, 15×1.56=23.5).

G.1.2.3. Injection frequency

As a matter of principle, it would have been valuable to adopt the methods set out above to perform another synthesis of continuous data, to provide a coherent NMA estimating number of injections required in each regimen. However, data are much more sparsely reported for this outcome and, even when we imputed as many datapoints as possible, we were unable to derive an evidence network in which a computationally tractable synthesis could be performed. For this reason, we were compelled to use a more naïve method when estimating injection frequency in our health economic model (see appendix J).

G.1.3. Ordered categorical variables

Another way of reporting change in BCVA is as the proportion of participants experiencing gains or losses of various magnitudes (e.g. the proportion of people gaining 15 or more letters). Outcomes such as these can be synthesised as a series of conditional probabilities, incorporating data on all reported levels of response (network meta-analysis for ordered categorical data using a generalised linear model with a binomial likelihood and a probit link function; see NICE DSU TSD2 [Dias et al. 2011a] for technical details).

Relative effects are estimated as z-scores – standard deviations on a standard normal distribution – which can then be converted into probabilities. Although we assume, elsewhere in the analysis undertaken for this guideline, that mean change in BCVA is likely to be normally distributed, the synthesis model adopted here does not imply any assumption about the distribution of the underlying variable, despite its use of the standard normal distribution. The model treats inter-category thresholds as arbitrary and estimates response probabilities from the response data alone; the actual magnitude of BCVA changes (e.g. 15 letters) is not an input to the calculation.

All categorical data were expressed in consecutive, mutually exclusive categories. This frequently entailed cosmetic manipulation of published data. For example, an RCT might report the proportion of people gaining 15 or more letters, the proportion of people losing 15 or more letters, and the proportion of people losing 30 or more letters. Such data were reordered to provide probabilities of change in the following categories:

\begin{array}{l} change & \leq & - 30 \\ - 30 & < & change & \leq & - 15 \\ - 15 & < & change & < & + 15 \\ + 15 & \leq & change \end{array}

Two versions of the analyses were performed. In the 5-category version, changes were analysed in 15-letter ‘bins’ that relied on the cut-offs most commonly reported in the included evidence:

\begin{array}{l} change & \leq & - 30 \\ - 30 & < & change & \leq & - 15 \\ - 15 & < & change & < & + 15 \\ - 15 & < & change & < & + 30 \\ + 30 & \leq & change \end{array}

In the 10-category version, changes were analysed in unequally spaced categories that made use of every cut-off reported in at least 1 trial:

\begin{array}{l} change & \leq & - 30 \\ - 30 & < & change & \leq & - 15 \\ - 15 & < & change & \leq & - 10 \\ - 10 & < & change & \leq & - 5 \\ - 5 & < & change & < & 0 \\ 0 & \leq & change & < & + 5 \\ + 5 & \leq & change & < & + 10 \\ + 10 & \leq & change & < & + 15 \\ + 15 & \leq & change & < & + 30 \\ + 30 & \leq & change \end{array}

The data were then combined using a model in which the probability (p) of patients in arm j of trial i achieving category k is modelled as

p_{i j k} = Φ (μ_{i 1} + z_{k} + δ_{i, j}),

(15)

where Φ represents the cumulative distribution function of the standard normal distribution, μ_i1 is the trial-specific baseline probability of achieving the first response category with the ‘control’ treatment, z_k represents the differences on the standard normal scale between the response to category k and the response to category k−1, and δ_i,j is the trial-specific treatment effect of the treatment in arm j relative to the treatment in arm 1 (defined as per (1) or (2) for fixed- and random-effects models, respectively).

In addition to inter-study fixed and random effects, we explored fixed- and random-effects approaches to estimation of the z-score cutpoints. When a random-effects model is adopted, each cutpoint z_k is calculated as the cutpoint for category k−1 plus a term representing the difference between the 2 categories, drawn from a lognormal distribution (in order to keep terms positive, as the z-score for a cutpoint cannot be less than the z-score for a category below it).

G.1.4. Dichotomous variables

One dichotomous variable – probability of discontinuation – was synthesised. We used a standard model with a binomial likelihood and logit link function (see NICE DSU TSD2 [Dias et al. 2011a]). In this formulation, the log-odds (that is, the logit of the probability, p) of the event occurring in arm j of trial i are estimated as

logit (p_{i, j}) = μ_{i} + δ_{i, j},

(16)

where δ_i,j is the trial-specific effect of the treatment in arm j relative to the treatment in arm 1 (defined as per (1) or (2) for fixed- and random-effects models, respectively). Meta-regression terms may be added to the linear predictor, as per (4).

We performed a single analysis, estimating the probability of discontinuation at 1 year (this was used to inform the constant rate of discontinuations incorporated in the health economic model; see appendix J). In theory, it would be attractive to model 1-year and 2-year discontinuations together, with 2-year probabilities formulated as conditional on nondiscontinuation in year 1 (see Lu et al. 2007). However, data were somewhat inconsistently reported, in this area, so a simple approach was preferred.

G.2. Results

G.2.1. Best-corrected visual acuity

G.2.1.1. Mean change

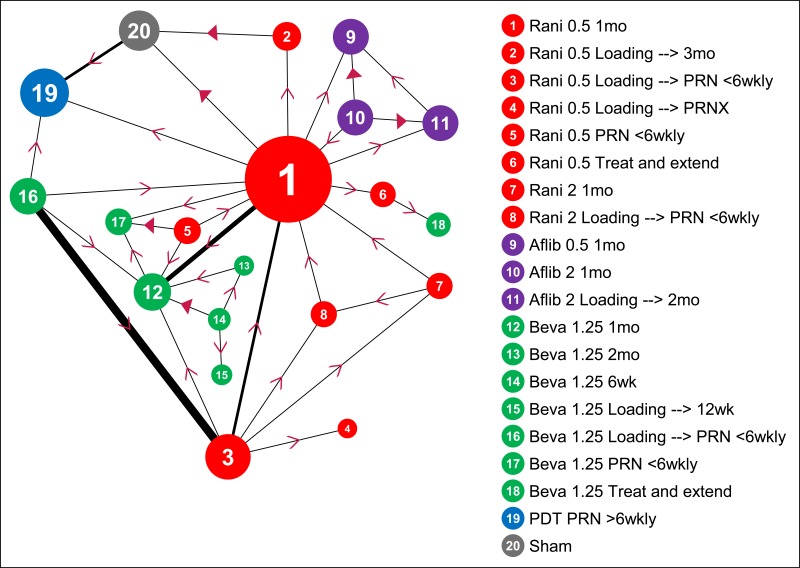
Regardless of model chosen (WMD -v- SMD; discrete nodes -v- meta-regression), the basic network and input data for all mean change syntheses are as shown in Figure 1 and Table 2, respectively.

The following features are clear:

Ranibizumab 0.5mg monthly is the node with most evidence at both 12 months and 24 months, and the option that has been compared with the greatest number of alternatives (this is why it was chosen as the reference option in our NMAs; see G.1.1).
There are relatively few data directly comparing PDT with anti-VEGFs (unsurprisingly, given when the various treatments were developed, most PDT evidence is versus sham). Relatedy, there are relatively few data directly comparing anti-VEGF and sham.
There are no 2-year data for routine anti-VEGF injection frequencies other than monthly. All 2-year anti-VEGF data relate to routine monthly, treat-and-extend or PRN regimens (with or without an initial loading phase).
Treat-and-extend regimens have only been trialled for bevacizumab and ranibizumab.
PRN-and-extend has only been evaluated in 1 small, 1-year RCT using ranibizumab. There are no 2-year data for this approach.
There are no prima facie incoherent loops of evidence in the network (e.g. where a > b, b > c and c > a).

Figure 1BCVA: mean change at 12 and 24 months – evidence network

Size of nodes is proportional to total number of participants randomised to receive the treatment in question across the evidence-base. Width of connecting lines is proportional to number of trial-level comparisons available. Arrowheads indicate direction of effect in pairwise data (a > b denotes a is more effective than b) – filled arrowheads show comparisons where one option is significantly superior (p<0.05); outlined arrowheads show direction of trend where effect does not reach statistical significance.

Table 2BCVA: mean change at 12 and 24 months – input data

	Aflib\|0.5\|1mo	Aflib\|0.5\|Loading --> PRN <6wkly	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Aflib\|2\|Loading --> PRN <6wkly	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|PRN <6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham anti-VEGF	Sham PDT
12 months
NATTB 2013								12.58 (13.88)	10.06 (16.00)
ANCHOR 2006													−9.50 (16.00)	9.90 (14.60)
Barikian 2015										8.00 (10.40)	8.30 (6.70)
BISWAS 2011										0.52 (15.63)						3.22 (12.01)
BRAMD 2016 (naïve)						6.06 (13.67)								6.82 (12.63)
CATT 2011						8.00 (15.80)					5.90 (15.70)			8.50 (14.10)				6.80 (13.10)
El-Mollayess						11.00 (10.46)					9.20 (14.72)
EXCITE 2010														8.00 (11.27)	3.41 (14.35)
GEFAL 2013										4.82 (14.85)						2.93 (15.09)
HARBOR														10.10 (13.30)		8.20 (13.30)				9.20 (14.60)	8.60 (13.80)
IVAN 2013						4.40 (13.20)				5.10 (11.40)				7.80 (14.20)		5.10 (10.40)
LUCAS 2015												7.90 (13.40)							8.20 (12.50)
Lushchyk 2013						1.90 (13.80)	6.00 (8.90)	1.60 (11.00)
MANTA 2013										4.90 (15.20)						4.10 (15.31)
MARINA														6.85 (13.59)								−10.40 (16.97)
PIER															−0.89 (14.12)							−16.30 (22.30)
Sacu 2009										8.00 (11.22)			−3.00 (15.53)
SALUTE 2015																3.20 (20.90)	7.70 (15.90)
Subramanian 2010										7.60 (15.38)						6.29 (13.74)
TREND 2017														8.10 (12.58)					6.20 (12.52)
TREX 2015														9.20 (16.21)					10.50 (10.73)
VIEW 1&2 POOLED	8.29 (13.75)		9.24 (13.21)	8.40 (14.70)										8.74 (14.45)
VIO													−11.20 (18.75)										−13.30 (15.34)
TAP 1999													−11.00 (20.19)										−17.50 (20.75)
VIM 2005													−8.50 (16.06)										−14.50 (18.13)
VIP 2001 Occ only													−15.60 (20.77)										−20.80 (22.45)
24 months
ANCHOR 2006													−9.80 (17.60)	9.40 (16.35)
CATT 2011						7.80 (15.50)					5.00 (17.90)			8.80 (15.90)				6.70 (14.60)
HARBOR														9.10 (14.90)		7.90 (14.70)				8.00 (17.40)	7.60 (15.30)
IVAN 2013						3.60 (15.20)				4.50 (11.50)				7.30 (15.20)		2.60 (14.40)
LUCAS 2015												7.40 (16.00)							6.60 (15.20)
MARINA														6.00 (15.13)								−14.90 (18.90)
TREX 2015														10.50 (8.27)					8.70 (17.26)
VIEW 1&2 POOLED		6.59 (15.21)			7.62 (15.81)											7.89 (16.11)
VIO													−14.80 (20.30)										−17.78 (16.71)
TAP 1999													−13.40 (21.79)										−19.60 (21.86)
VIM 2005													−16.00 (20.01)										−21.00 (22.50)
VIP 2001 Occ only													−19.00 (22.57)										−25.50 (22.55)

: Values are mean change from baseline to follow up (SD). Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

G.2.1.1.1. Mean difference at 12 and 24 months (bivariate normal likelihood)

G.2.1.1.1.1. Model selection

A wide variety of models was explored for this outcome, as it provided the most complete summary of available effectiveness data, and it was critical for the parameterisation of the health economic model.

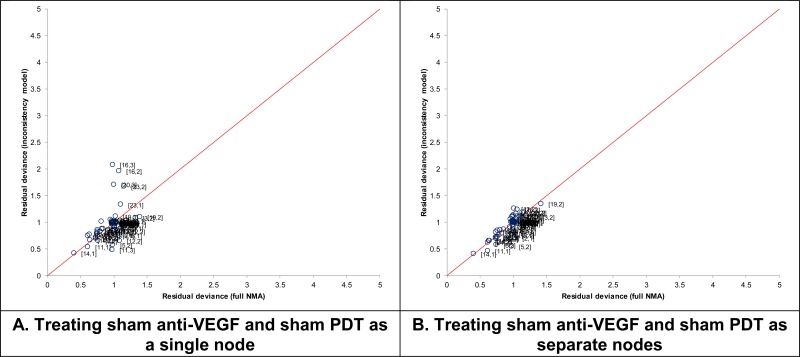
The first choice we made was to separate ‘sham anti-VEGF’ and ‘sham-PDT’ nodes in the networks. This was because preliminary exploration showed that there was inconsistency associated with RCTs of PDT -v- sham, when ‘sham’ was treated as a single node (see Figure 2A). This problem was resolved when the node was separated into its 2 component elements (see Figure 2B), and measure of model fit, including DIC and residual deviance (not shown), were also improved. Therefore, we concluded this was a superior approach, and treated ‘sham anti-VEGF’ and ‘sham-PDT’ as separate entities.

Figure 2Comparison of residual deviance between full NMA and inconsistency model, when sham anti-VEGF and sham PDT are treated as (A) a single node or (B) separate nodes

‘Split’ network with 22 (A) or 23 (B) nodes. See NICE DSU TSD 4 for methods and technical explanation of the inconsistency model.

This gave us a network with up to 23 agent–dose–regimen triads. To help illustrate the features of the evidence network, we provide outputs of a ‘split’ NMA (that is, one with a discrete node for every agent–dose–regimen triad, amounting to 23 nodes) on the natural (mean difference in ETDRS letters) scale in 0.

Summary fit statistics for each model are given in Table 3. Some features are immediately obvious: fixed-effects models always have higher residual deviance than their random-effects counterparts and adjusted (meta-regression) models have meaningfully superior DIC to their ‘split’, 23-node equivalents.

Therefore, there is strong justification for preferring a meta-regression model that, at a minimum, treats the effect of PRN administration as shared among all anti-VEGF agents. The value that is added by distinguishing between PRN regimens with and without loading phases is less apparent. DIC goes up somewhat and other measures of model fit are no better when the term is included. This is in keeping with the pairwise evidence showing that no difference between these approaches could be identified at 1 year (see full guideline 10.1.4.3.1). Nevertheless, we opted to retain this term in the model, as it was perceived to have potentially important consequences for the health economic analysis: if the term was dropped, we would have been forced either to model an average of loading and non-loading approaches (which it would not be straightforward to cost) or to state from the outset that pre-PRN loading has no value, and assume that such costs should never be incurred (this is also at odds with the SPC for ranibizumab).

Treating TREX and PRNX as shared covariates results in a very small improvement in model fit. As including these terms certainly did not harm the synthesis model, and it enabled the strategies to be entered into the health economic model in a flexible way (including the speculative exploration of PRNX and TREX regimens for agents in which they have not been empirically researched), we concluded they should be retained.

The most complicated decision was as regards how frequency of administration could best be represented. All 3 models that were explored showed slightly inferior DIC to models in which separate routine frequencies were treated as separate nodes. However, this requires close exploration.

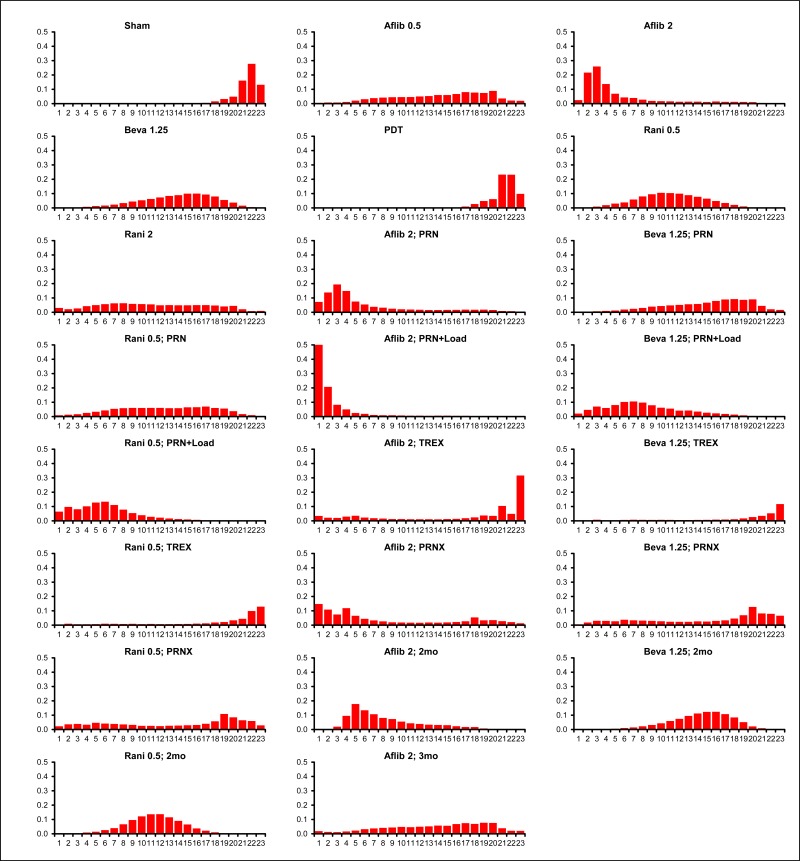
In particular, we noted that a single datapoint was having a large influence on the frequency-adjusted models. It can be seen, in 0 (most clearly shown in Figure 9), that the estimate for bevacizumab given at 2-monthly intervals presents an unexpectedly positive result. Elsewhere in that network, the expected frequency–response relationship is seen; for example, 6-weekly bevacizumab is slightly worse than monthly, and 3-monthly bevacizumab is worse again. However, the point-estimate for bevacizumab 2-monthly is that it is better than monthly treatment, and has a relatively high chance (>0.3) of being the most effective strategy in the split WMD network. We note that this finding is entirely consistent with expected levels of simple random sampling error – note that the credible intervals are wide and overlap in a way that makes the expected frequency–response relationship entirely plausible, at a 95% confidence level. On inspection of input data (see Table 2), it can be seen that this finding results from a single RCT (Lushchyk et al., 2013), in which the 2-monthly bevacizumab group (n=54) gained 6 ETDRS letters at 1 year, whereas the 1-monthly bevacizumab group (n=46) gained a little under 2 (a similar finding is evident in the categorical data – see Table 28). Again, we emphasise that there is no reason to believe this is a fundamentally biased finding – it is within the range of expected sampling error if there were no difference between the strategies (i.e. it is not a ‘significant’ difference). Nevertheless, it is one that would, on average, be propagated throughout the evidence if taken on face value. For example, if the split network were used as a basis for health economic analysis, 2-monthly bevacizumab would be sure to have a high probability of being optimal – it would be prominent in CEACs – even though the uncertainty attached to the estimate would also result in it having a (largely unseen) non-negligible probability of being a poor choice.

This kind of finding is a strong motivation for adopting a frequency–response model that seeks to establish what the average relationship between frequency and effect is throughout the network, and then combines that with what is known about monthly administration to arrive at an estimate that makes best use of all available data.

To explore this, we performed a series of sensitivity analyses in which the models were refitted to a dataset that excluded the single anomalous datapoint from Lushchyk et al. (2013). When we did this, we found that all frequency-adjusted models had a superior fit to the data, with DIC dropping by up to 5 points, compared with unadjusted models.

Therefore, we concluded that a frequency–response model provided the optimal representation of the evidence, and preferred this approach for our selected model for the full dataset. In this context, the fact that frequency-adjusted models have a slightly worse fit to the observed data is actually a desirable property, as the datapoint that they fit poorly is the one that was inconsistent with other data, showing that the approach has been effective in minimising the influence of the outlying estimate.

It was hard to distinguish between the 3 frequency–response models, and a good argument could be made for adopting the simplest – MR4a – which assumes that a single frequency–response effect is shared between all anti-VEGFs. However, the committee advised that most clinicians would have an a priori assumption that there would at least be a difference between aflibercept and the 2 monocolonal antibodies, with aflibercept providing slightly longer-lasting benefits. Therefore, we concluded it would be conservative to distinguish between these options, and model MR4c – which had very marginally better fit to the data that MR4b in the sensitivity analysis excluding the anomalous datapoint from Lushchyk et al. (2013) – was preferred.

In relection of all the above considerations, our final preferred choice for the 12- and 24-month mean difference synthesis was the random-effects model adjusting for PRN, pre-PRN loading, TREX, PRNX and frequency (with separate terms for aflibercept and monoclonal antibodies).

Although residual deviance was higher with fixed-effects models, they tended to be associated with DIC values that were at least equivalent to random-effects counterparts. This was particularly true for meta-regression approaches: fixed-effects models fitted the split data less well; however, introducing covariates explained a good deal of the heterogeneity. Because a case could be made for preferring the fixed-effects models, we captured the results from FIXED MR4c, and used it in a sensitivity analysis for our HE model.

Table 3BCVA: mean difference at 12 and 24 months – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	Between-study SD
91.77 (compared to 92 datapoints)	265.3	199.6	65.74	331.1	12 months: 0.71 (95%CrI: 0.03, 1.96) 24 months: 0.48 (95%CI: 0.03, 1.33)

Table 4BCVA: mean difference at 12 and 24 months – summary model fit statistics, showing selection of best-fitting model

Outcome	Model for treatment differences	Number of discrete nodes	Covariates					N	Total residual deviance	DIC	Standard deviation of random effects distributions (95%CrI)
Outcome	Model for treatment differences	Number of discrete nodes	PRN	Loading	TREX	PRNX	Frequency	N	Total residual deviance	DIC	0–12 months	12–24 months
Mean change in BCVA at 12 & 24 months	FIXED	23						99	103.40	356.3	n/a	n/a
	FIXED MR1	16	✓						94.12	341.0	n/a	n/a
	FIXED MR2	16	✓	✓					95.46	344.3	n/a	n/a
	FIXED MR3	13	✓	✓	✓	✓			94.90	341.9	n/a	n/a
	FIXED MR4a	8	✓	✓	✓	✓	✓		105.60	348.6	n/a	n/a
	FIXED MR4b	8	✓	✓	✓	✓	✓		103.90	348.9	n/a	n/a
	FIXED MR4c	8	✓	✓	✓	✓	✓		106.00	350.0	n/a	n/a
	RANDOM	23							93.88	355.7	0.53 (0.02, 1.86)	0.71 (0.09, 1.93)
	RANDOM MR1	16	✓						93.15	347.2	0.46 (0.02, 1.53)	0.47 (0.03, 1.29)
	RANDOM MR2	16	✓	✓					94.30	350.4	0.49 (0.02, 1.64)	0.49 (0.03, 1.33)
	RANDOM MR3	13	✓	✓	✓	✓			93.18	347.1	0.46 (0.02, 1.52)	0.49 (0.03, 1.31)
	RANDOM MR4a	8	✓	✓	✓	✓	✓		97.61	349.7	0.64 (0.04, 1.83)	0.49 (0.02, 1.29)
	RANDOM MR4b	8	✓	✓	✓	✓	✓		97.15	350.3	0.58 (0.02, 1.75)	0.49 (0.03, 1.29)
	RANDOM MR4c	8	✓	✓	✓	✓	✓		97.89	351.4	0.71 (0.04, 1.95)	0.49 (0.04, 1.30)
Mean change in BCVA at 12 & 24 months (sensitivity analysis excluding Bev 2mo from Lushchyk 2013)	FIXED	22						98	102.50	352.5	n/a	n/a
	FIXED MR1	15	✓						93.26	337.1	n/a	n/a
	FIXED MR2	15	✓	✓					94.63	340.5	n/a	n/a
	FIXED MR3	12	✓	✓	✓	✓			93.70	337.4	n/a	n/a
	FIXED MR4a	8	✓	✓	✓	✓	✓		95.97	336.8	n/a	n/a
	FIXED MR4b	8	✓	✓	✓	✓	✓		96.36	339.1	n/a	n/a
	FIXED MR4c	8	✓	✓	✓	✓	✓		95.60	337.5	n/a	n/a
	RANDOM	22							93.15	352.0	0.57 (0.02, 1.89)	0.70 (0.08, 1.92)
	RANDOM MR1	15	✓						92.01	342.7	0.45 (0.03, 1.52)	0.47 (0.03, 1.26)
	RANDOM MR2	15	✓	✓					93.17	346.2	0.55 (0.03, 1.69)	0.47 (0.03, 1.32)
	RANDOM MR3	12	✓	✓	✓	✓			92.05	342.6	0.49 (0.04, 1.54)	0.47 (0.04, 1.26)
	RANDOM MR4a	8	✓	✓	✓	✓	✓		90.89	338.8	0.43 (0.01, 1.36)	0.48 (0.03, 1.29)
	RANDOM MR4b	8	✓	✓	✓	✓	✓		91.30	341.2	0.45 (0.01, 1.47)	0.50 (0.05, 1.30)
	RANDOM MR4c	8	✓	✓	✓	✓	✓		91.04	340.1	0.43 (0.02, 1.42)	0.48 (0.04, 1.27)

: MR4a = 1 covariate shared between anti-VEGF agents for frequency–response effect; MR4b = separate covariates for each anti-VEGF agent for frequency–response effect; MR4c = 1 covariate for aflibercept and 1 covariate for bevacizumab and ranibizuamb for frequency–response effect;

G.2.1.1.1.2. 12 months

Table 5BCVA: mean difference at 12 months – relative effectiveness of all pairwise combinations

Sham

17.0 (13.3, 20.7)

Aflib 0.5

18.7 (13.7, 23.8)

1.8 (−2.4, 6.0)

Aflib 2

18.6 (15.1, 22.0)

1.6 (−1.5, 4.6)

−0.2 (−4.9, 4.4)

Beva 1.25

−1.3 (−5.5, 3.1)

−18.2 (−22.4, −14.1)

−20.0 (−25.4, −14.5)

−19.8 (−23.5, −16.1)

PDT

19.0 (15.8, 22.2)

2.0 (−0.9, 4.8)

0.2 (−4.3, 4.6)

0.4 (−0.8, 1.6)

20.2 (16.6, 23.7)

Rani 0.5

17.2 (13.8, 20.7)

0.2 (−3.1, 3.5)

−1.6 (−6.3, 3.2)

−1.4 (−4.0, 1.3)

18.4 (14.5, 22.4)

−1.8 (−4.2, 0.7)

Rani 2

−5.9 (−10.9, −1.0)

−22.9 (−27.8, −18.0)

−24.7 (−30.7, −18.8)

−24.5 (−28.9, −20.0)

−4.7 (−7.1, −2.3)

−24.9 (−29.3, −20.6)

−23.2 (−27.8, −18.5)

Sham PDT

17.3 (12.1, 22.7)

0.3 (−4.2, 4.8)

−1.5 (−3.1, 0.2)

−1.3 (−6.1, 3.8)

18.6 (12.9, 24.1)

−1.7 (−6.3, 3.2)

0.1 (−4.9, 5.2)

23.2 (17.1, 29.4)

Aflib 2 PRN

17.1 (13.4, 20.8)

0.2 (−3.3, 3.6)

−1.6 (−6.5, 3.2)

−1.5 (−3.1, 0.2)

18.4 (14.3, 22.3)

−1.9 (−3.8, 0.1)

−0.1 (−3.2, 3.0)

23.1 (18.3, 27.8)

−0.2 (−4.9, 4.4)

Beva 1.25 PRN

17.5 (13.9, 21.1)

0.5 (−2.7, 3.8)

−1.2 (−6.1, 3.4)

−1.1 (−3.2, 1.1)

18.8 (14.8, 22.7)

−1.5 (−3.1, 0.2)

0.3 (−2.7, 3.3)

23.5 (18.8, 28.1)

0.2 (−4.3, 4.6)

0.4 (−0.8, 1.6)

Rani 0.5 PRN

17.4 (12.2, 22.7)

0.5 (−4.1, 4.9)

−1.3 (−2.9, 0.1)

−1.2 (−5.9, 3.7)

18.7 (13.0, 24.2)

−1.6 (−6.2, 3.2)

0.2 (−4.8, 5.2)

23.4 (17.2, 29.4)

0.1 (−2.0, 2.2)

0.3 (−4.7, 5.4)

−0.1 (−5.0, 4.9)

Aflib 2 PRNL

17.3 (13.5, 20.9)

0.3 (−3.2, 3.6)

−1.5 (−6.5, 3.3)

−1.3 (−2.9, 0.1)

18.5 (14.5, 22.4)

−1.7 (−3.6, 0.1)

0.0 (−3.1, 3.1)

23.2 (18.5, 27.8)

0.0 (−5.3, 5.0)

0.1 (−2.0, 2.2)

−0.3 (−2.8, 2.2)

−0.2 (−4.9, 4.4)

Beva 1.25 PRNL

17.7 (14.1, 21.1)

0.7 (−2.5, 3.8)

−1.1 (−5.9, 3.5)

−0.9 (−2.8, 1.0)

18.9 (15.1, 22.7)

−1.3 (−2.9, 0.1)

0.4 (−2.5, 3.3)

23.6 (19.0, 28.1)

0.4 (−4.7, 5.2)

0.5 (−1.8, 2.8)

0.1 (−2.0, 2.2)

0.2 (−4.3, 4.6)

0.4 (−0.8, 1.6)

Rani 0.5 PRNL

17.4 (12.0, 23.3)

0.5 (−4.2, 5.5)

−1.3 (−3.5, 1.2)

−1.2 (−6.2, 4.3)

18.7 (12.9, 24.8)

−1.5 (−6.4, 3.7)

0.2 (−5.0, 5.7)

23.4 (17.1, 29.9)

0.2 (−2.6, 3.2)

0.3 (−4.9, 5.9)

−0.1 (−5.2, 5.4)

0.0 (−2.6, 3.0)

0.2 (−5.1, 5.9)

−0.2 (−5.3, 5.3)

Aflib 2 TREX

17.3 (13.2, 21.5)

0.3 (−3.5, 4.3)

−1.5 (−6.6, 3.8)

−1.3 (−3.5, 1.2)

18.6 (14.1, 22.9)

−1.7 (−4.2, 1.0)

0.1 (−3.4, 3.8)

23.2 (18.2, 28.3)

0.0 (−5.4, 5.5)

0.2 (−2.6, 3.2)

−0.2 (−3.3, 3.0)

−0.2 (−5.5, 5.4)

0.0 (−2.6, 3.0)

−0.4 (−3.3, 2.8)

−0.2 (−4.9, 4.4)

Beva 1.25 TREX

17.7 (13.7, 21.7)

0.7 (−2.9, 4.5)

−1.1 (−6.1, 4.1)

−0.9 (−3.4, 1.9)

18.9 (14.7, 23.2)

−1.3 (−3.5, 1.2)

0.5 (−2.9, 4.0)

23.6 (18.7, 28.6)

0.4 (−4.9, 5.7)

0.5 (−2.4, 3.7)

0.2 (−2.6, 3.2)

0.2 (−5.0, 5.6)

0.4 (−2.5, 3.6)

0.0 (−2.6, 3.0)

0.2 (−4.3, 4.6)

0.4 (−0.8, 1.6)

Rani 0.5 TREX

21.9 (12.1, 31.6)

4.9 (−4.5, 14.4)

3.1 (−5.4, 11.5)

3.3 (−6.3, 13.0)

23.1 (13.1, 33.1)

2.9 (−6.6, 12.5)

4.7 (−5.1, 14.4)

27.8 (17.5, 38.2)

4.6 (−4.1, 13.1)

4.7 (−4.9, 14.4)

4.3 (−5.3, 14.0)

4.4 (−3.9, 12.7)

4.6 (−4.9, 14.2)

4.2 (−5.2, 13.7)

4.4 (−4.5, 13.1)

4.6 (−5.4, 14.5)

4.2 (−5.7, 14.0)

Aflib 2 PRNX

21.7 (12.6, 30.7)

4.7 (−4.3, 13.7)

2.9 (−6.8, 12.5)

3.1 (−5.4, 11.5)

22.9 (13.7, 32.1)

2.7 (−5.9, 11.2)

4.5 (−4.5, 13.3)

27.6 (18.1, 37.1)

4.4 (−5.4, 14.1)

4.6 (−4.1, 13.1)

4.2 (−4.6, 12.8)

4.2 (−5.4, 13.7)

4.4 (−3.9, 12.7)

4.0 (−4.4, 12.4)

4.2 (−5.8, 14.0)

4.4 (−4.5, 13.1)

4.0 (−4.9, 12.8)

−0.2 (−4.9, 4.4)

Beva 1.25 PRNX

22.1 (13.1, 31.1)

5.1 (−3.8, 14.0)

3.3 (−6.3, 12.7)

3.5 (−5.1, 12.1)

23.3 (14.1, 32.5)

3.1 (−5.4, 11.5)

4.9 (−4.0, 13.6)

28.0 (18.5, 37.4)

4.8 (−5.0, 14.3)

5.0 (−3.7, 13.6)

4.6 (−4.1, 13.1)

4.6 (−4.8, 14.1)

4.8 (−3.6, 13.3)

4.4 (−3.9, 12.7)

4.6 (−5.4, 14.4)

4.8 (−4.2, 13.6)

4.4 (−4.5, 13.1)

0.2 (−4.3, 4.6)

0.4 (−0.8, 1.6)

Rani 0.5 PRNX

17.9 (14.3, 21.6)

0.9 (−1.5, 3.4)

−0.8 (−3.3, 1.7)

−0.7 (−3.6, 2.4)

19.2 (15.0, 23.3)

−1.1 (−3.8, 1.8)

0.7 (−2.6, 4.0)

23.9 (19.1, 28.7)

0.6 (−2.4, 3.6)

0.8 (−2.5, 4.2)

0.4 (−2.8, 3.7)

0.5 (−2.4, 3.4)

0.7 (−2.6, 4.1)

0.3 (−2.8, 3.5)

0.5 (−3.1, 3.8)

0.6 (−3.3, 4.4)

0.3 (−3.5, 3.8)

−3.9 (−12.8, 4.9)

−3.7 (−12.6, 5.3)

−4.1 (−12.9, 4.8)

Aflib 2 2mo

17.0 (14.1, 20.0)

0.1 (−2.7, 2.8)

−1.7 (−6.2, 2.7)

−1.5 (−2.8, −0.3)

18.3 (14.7, 21.8)

−1.9 (−3.7, −0.2)

−0.2 (−2.6, 2.2)

23.0 (18.7, 27.2)

−0.2 (−5.1, 4.5)

−0.1 (−2.2, 2.0)

−0.5 (−3.0, 2.0)

−0.4 (−5.0, 4.2)

−0.2 (−2.1, 1.8)

−0.6 (−2.9, 1.7)

−0.4 (−5.6, 4.5)

−0.3 (−3.0, 2.4)

−0.6 (−3.6, 2.2)

−4.8 (−14.4, 4.7)

−4.6 (−13.1, 4.0)

−5.0 (−13.6, 3.7)

−0.9 (−3.6, 1.9)

Beva 1.25 2mo

17.4 (14.7, 20.2)

0.5 (−2.1, 3.0)

−1.3 (−5.6, 2.9)

−1.1 (−2.8, 0.6)

18.7 (15.3, 22.0)

−1.5 (−2.8, −0.3)

0.2 (−1.9, 2.3)

23.4 (19.2, 27.6)

0.1 (−4.5, 4.6)

0.3 (−1.9, 2.6)

−0.1 (−2.2, 2.0)

0.0 (−4.5, 4.5)

0.2 (−2.0, 2.5)

−0.2 (−2.1, 1.8)

0.0 (−5.0, 4.8)

0.1 (−2.8, 3.0)

−0.3 (−3.0, 2.4)

−4.4 (−13.9, 5.1)

−4.2 (−12.8, 4.4)

−4.6 (−13.1, 4.0)

−0.5 (−3.0, 2.0)

0.4 (−0.8, 1.6)

Rani 0.5 2mo

17.1 (13.4, 20.8)

0.1 (−2.4, 2.7)

−1.7 (−6.6, 3.4)

−1.5 (−4.5, 1.6)

18.4 (14.2, 22.5)

−1.9 (−4.7, 1.0)

−0.1 (−3.4, 3.1)

23.0 (18.1, 27.8)

−0.2 (−5.5, 5.0)

0.0 (−3.4, 3.4)

−0.4 (−3.7, 2.9)

−0.3 (−5.5, 4.9)

−0.2 (−3.4, 3.3)

−0.6 (−3.6, 2.7)

−0.3 (−6.0, 5.1)

−0.2 (−4.1, 3.6)

−0.6 (−4.3, 3.1)

−4.8 (−14.5, 5.0)

−4.6 (−13.5, 4.4)

−5.0 (−13.8, 4.0)

−0.8 (−3.3, 1.7)

0.1 (−2.7, 2.8)

−0.3 (−2.9, 2.2)

Aflib 2 3mo

15.5 (12.5, 18.5)

−1.5 (−4.4, 1.6)

−3.3 (−7.8, 1.3)

−3.1 (−5.6, −0.5)

16.8 (13.0, 20.5)

−3.5 (−6.2, −0.6)

−1.7 (−4.4, 1.0)

21.4 (16.9, 25.9)

−1.8 (−6.7, 3.1)

−1.6 (−4.6, 1.4)

−2.0 (−5.3, 1.4)

−1.9 (−6.7, 2.9)

−1.8 (−4.6, 1.2)

−2.1 (−5.3, 1.1)

−1.9 (−7.2, 3.2)

−1.8 (−5.3, 1.6)

−2.2 (−5.9, 1.4)

−6.3 (−16.0, 3.3)

−6.2 (−14.9, 2.7)

−6.5 (−15.4, 2.4)

−2.4 (−5.4, 0.6)

−1.5 (−2.8, −0.3)

−1.9 (−3.7, −0.2)

−1.6 (−4.6, 1.5)

Beva 1.25 3mo

15.9 (13.1, 18.7)

−1.1 (−3.8, 1.8)

−2.9 (−7.2, 1.6)

−2.7 (−5.4, 0.2)

17.1 (13.5, 20.7)

−3.1 (−5.6, −0.5)

−1.3 (−3.7, 1.2)

21.8 (17.5, 26.2)

−1.4 (−6.1, 3.3)

−1.2 (−4.3, 2.0)

−1.6 (−4.6, 1.4)

−1.5 (−6.1, 3.2)

−1.4 (−4.4, 1.8)

−1.8 (−4.6, 1.2)

−1.5 (−6.7, 3.4)

−1.4 (−5.1, 2.2)

−1.8 (−5.3, 1.6)

−6.0 (−15.5, 3.6)

−5.8 (−14.7, 3.2)

−6.2 (−14.9, 2.7)

−2.0 (−4.7, 0.8)

−1.1 (−2.8, 0.6)

−1.5 (−2.8, −0.3)

−1.2 (−4.0, 1.6)

0.4 (−0.8, 1.6)

Rani 0.5 3mo

: Values given are mean differences in ETDRS letters (row versus column; i.e. negative numbers favour the option above and positive numbers favour the option on the right). Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

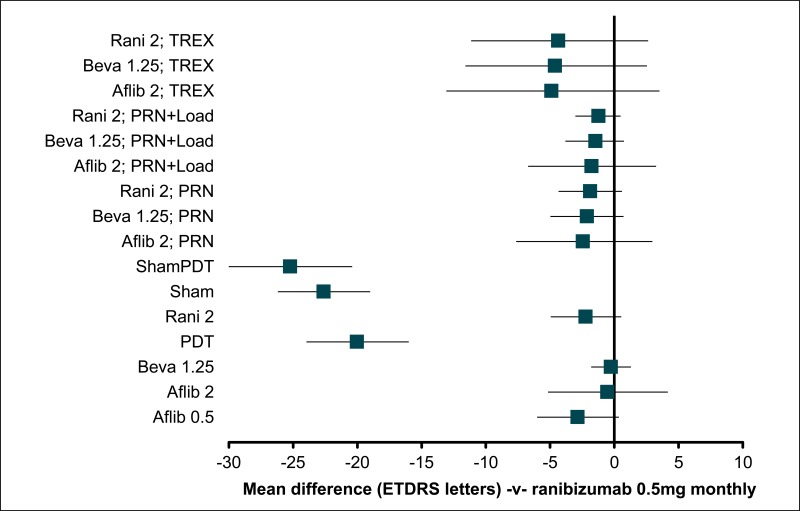
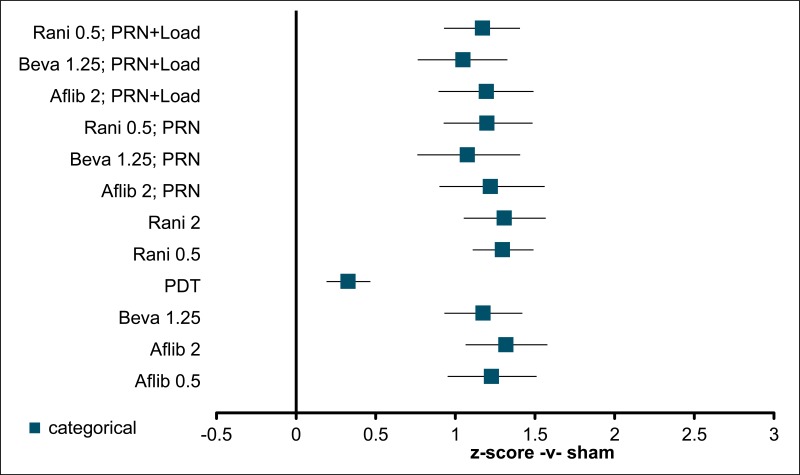
Figure 3BCVA: mean difference at 12 months – relative effect of all options versus sham anti-VEGF

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 4BCVA: mean difference at 12 months – expected absolute change

Table 6BCVA: mean difference at 12 months – meta-regression coefficients

Covariate		Beta	(95%CrI)
PRN		−1.45	(−3.11, 0.22)
Loading		0.12	(−2.00, 2.21)
TREX		−1.28	(−3.54, 1.21)
PRNX		4.41	(−3.93, 12.73)
Frequency (per additional month)	Aflibercept	−0.83	(−3.32, 1.69)
Frequency (per additional month)	Bevacizumab / ranibizumab	−1.54	(−2.79, −0.25)

: Values on natural scale (ETDRS letters); negative values indicate worse BCVA

Table 7BCVA: mean difference at 12 months – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	24 (24, 25)
Aflib 0.5	0.005	16 (4, 23)
Aflib 2	0.082	5 (1, 20)
Beva 1.25	0.027	6 (1, 15)
PDT	0.000	25 (24, 25)
Rani 0.5	0.069	5 (1, 12)
Rani 2	0.009	14 (3, 23)
ShamPDT	0.000	26 (26, 26)
Aflib 2; PRN	0.004	14 (3, 23)
Beva 1.25; PRN	0.001	15 (5, 23)
Rani 0.5; PRN	0.004	12 (4, 22)
Aflib 2; PRN+Load	0.002	13 (3, 23)
Beva 1.25; PRN+Load	0.001	14 (5, 22)
Rani 0.5; PRN+Load	0.002	12 (4, 21)
Aflib 2; TREX	0.017	13 (2, 23)
Beva 1.25; TREX	0.006	14 (3, 23)
Rani 0.5; TREX	0.014	11 (2, 22)
Aflib 2; PRNX	0.330	3 (1, 23)
Beva 1.25; PRNX	0.110	3 (1, 23)
Rani 0.5; PRNX	0.309	2 (1, 22)
Aflib 2; 2mo	0.000	10 (4, 18)
Beva 1.25; 2mo	0.000	15 (7, 21)
Rani 0.5; 2mo	0.000	13 (6, 19)
Aflib 2; 3mo	0.010	15 (3, 23)
Beva 1.25; 3mo	0.000	22 (12, 23)
Rani 0.5; 3mo	0.000	21 (10, 23)

Figure 5BCVA: mean difference at 12 months – rank probability histograms

Histograms show probability that each treatment is ranked in each position relative to the other treatments in the network. Rank 1 always refects whatever is desirable (a high probability of good outcomes or a low probability of bad outcomes).

G.2.1.1.1.3. 24 months

Table 8BCVA: mean difference at 24 months – relative effectiveness of all pairwise combinations

Sham

19.8 (15.5,24.1)

Aflib 0.5

22.1 (16.6,27.5)

2.3 (−2.1,6.7)

Aflib 2

22.4 (18.5,26.3)

2.6 (−1.0,6.1)

0.3 (−4.7,5.1)

Beva 1.25

2.6 (−2.3,7.6)

−17.2 (−21.9,-12.4)

−19.5 (−25.3,-13.6)

−19.8 (−24.0,-15.5)

PDT

22.6 (19.0,26.2)

2.9 (−0.4,6.0)

0.5 (−4.2,5.2)

0.3 (−1.3,1.8)

20.0 (16.0,24.0)

Rani 0.5

20.4 (16.4,24.4)

0.6 (−3.2,4.4)

−1.7 (−6.8,3.4)

−2.0 (−5.1,1.2)

17.8 (13.2,22.3)

−2.2 (−5.0,0.5)

Rani 2

−2.6 (−8.3,3.1)

−22.4 (−27.8,-16.9)

−24.7 (−31.1,-18.2)

−25.0 (−30.0,-19.9)

−5.2 (−7.8,-2.6)

−25.2 (−30.1,-20.4)

−23.0 (−28.3,-17.7)

ShamPDT

20.2 (14.3,26.2)

0.4 (−4.6,5.5)

−1.9 (−4.3,0.6)

−2.2 (−7.6,3.5)

17.6 (11.2,23.9)

−2.4 (−7.6,3.0)

−0.2 (−5.9,5.5)

22.8 (15.9,29.7)

Aflib 2; PRN

20.5 (15.9,25.1)

0.7 (−3.5,5.0)

−1.6 (−7.1,3.8)

−1.9 (−4.3,0.6)

17.9 (13.0,22.8)

−2.1 (−5.0,0.7)

0.1 (−3.9,4.1)

23.1 (17.5,28.7)

0.3 (−4.7,5.1)

Beva1.25; PRN

20.7 (16.4,25.1)

1.0 (−3.1,5.0)

−1.3 (−6.6,3.9)

−1.6 (−4.6,1.3)

18.1 (13.5,22.9)

−1.9 (−4.3,0.6)

0.3 (−3.4,4.0)

23.4 (17.9,28.8)

0.5 (−4.2,5.2)

0.3 (−1.3,1.8)

Rani 0.5; PRN

20.9 (15.1,26.6)

1.1 (−3.6,5.8)

−1.2 (−3.0,0.5)

−1.5 (−6.7,3.8)

18.3 (12.0,24.2)

−1.8 (−6.7,3.3)

0.5 (−5.0,5.8)

23.5 (16.7,30.0)

0.6 (−2.3,3.5)

0.4 (−5.3,6.1)

0.1 (−5.3,5.6)

Aflib 2; PRNL

21.1 (16.9,25.3)

1.4 (−2.6,5.2)

−0.9 (−6.2,4.2)

−1.2 (−3.0,0.5)

18.6 (14.0,23.0)

−1.5 (−3.8,0.7)

0.7 (−2.9,4.3)

23.7 (18.5,29.0)

0.9 (−4.9,6.5)

0.6 (−2.3,3.5)

0.4 (−2.9,3.6)

0.3 (−4.7,5.1)

Beva1.25; PRNL

21.4 (17.3,25.3)

1.6 (−2.1,5.2)

−0.7 (−5.8,4.2)

−1.0 (−3.4,1.4)

18.8 (14.5,23.0)

−1.2 (−3.0,0.5)

1.0 (−2.4,4.2)

24.0 (18.9,29.0)

1.2 (−4.4,6.6)

0.9 (−2.5,4.1)

0.6 (−2.3,3.5)

0.5 (−4.2,5.2)

0.3 (−1.3,1.8)

Rani 0.5; PRNL

17.7 (9.1,26.6)

−2.0 (−10.0,6.2)

−4.4 (−11.2,2.6)

−4.7 (−12.9,4.0)

15.1 (6.1,24.2)

−4.9 (−13.1,3.5)

−2.7 (−11.1,5.9)

20.4 (11.0,29.7)

−2.5 (−9.7,4.9)

−2.8 (−11.4,6.1)

−3.0 (−11.6,5.7)

−3.1 (−10.1,4.0)

−3.4 (−11.9,5.3)

−3.7 (−12.0,4.9)

Aflib 2; TREX

18.0 (10.2,26.0)

−1.8 (−9.4,6.1)

−4.1 (−12.4,4.4)

−4.4 (−11.2,2.6)

15.4 (7.4,23.5)

−4.6 (−11.6,2.5)

−2.4 (−9.9,5.2)

20.7 (12.2,29.2)

−2.2 (−10.9,6.6)

−2.5 (−9.7,4.9)

−2.7 (−10.1,4.8)

−2.8 (−11.4,5.9)

−3.1 (−10.1,4.0)

−3.4 (−10.6,4.0)

0.28 (−4.73,5.13)

Beva1.25; TREX

18.2 (10.7,26.1)

−1.5 (−9.0,6.2)

−3.8 (−12.0,4.5)

−4.1 (−11.1,3.1)

15.7 (7.8,23.7)

−4.4 (−11.2,2.6)

−2.1 (−9.4,5.3)

20.9 (12.5,29.3)

−2.0 (−10.5,6.7)

−2.2 (−9.6,5.4)

−2.5 (−9.7,4.9)

−2.6 (−10.9,6.0)

−2.8 (−10.1,4.4)

−3.1 (−10.1,4.0)

0.55 (−4.17,5.16)

0.26 (−1.29,1.80)

Rani 0.5; TREX

: Values given are mean differences (negative numbers favour the option above; positive numbers favour the option on the right)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

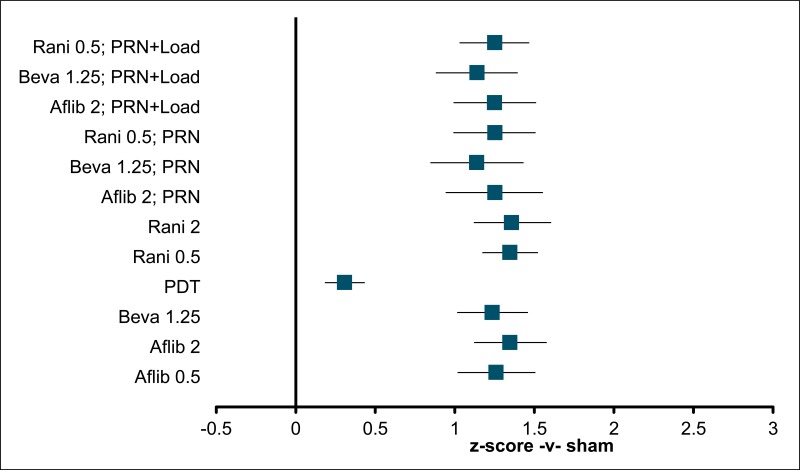
Figure 6BCVA: mean difference at 24 months – relative effect of all options versus sham anti-VEGF

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 7BCVA: mean difference at 24 months – expected absolute change

Table 9BCVA: mean difference at 12 months – meta-regression coefficients

Covariate	Beta	(95%CrI)
PRN	−1.88	(−4.35, 0.59)
Load	0.64	(−2.28, 3.55)
TREX	−4.33	(−11.15, 2.62)

: Values on natural scale (ETDRS letters); negative values indicate worse BCVA

Table 10BCVA: mean difference at 24 months – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	16 (15, 17)
Aflib 0.5	0.008	10 (3, 14)
Aflib 2	0.275	4 (1, 11)
Beva 1.25	0.192	3 (1, 9)
PDT	0.000	15 (15, 16)
Rani 0.5	0.278	2 (1, 7)
Rani 2	0.022	9 (2, 14)
ShamPDT	0.000	17 (16, 17)
Aflib 2; PRN	0.022	9 (2, 14)
Beva 1.25; PRN	0.012	8 (2, 14)
Rani 0.5; PRN	0.019	8 (2, 13)
Aflib 2; PRN+Load	0.025	7 (1, 13)
Beva 1.25; PRN+Load	0.015	7 (2, 13)
Rani 0.5; PRN+Load	0.027	6 (1, 12)
Aflib 2; TREX	0.038	12 (1, 14)
Beva 1.25; TREX	0.026	12 (1, 14)
Rani 0.5; TREX	0.040	12 (1, 14)

Figure 8BCVA: mean difference at 24 months – rank probability histograms

G.2.1.1.2. Mean difference at 12 and 24 months (bivariate normal likelihood) – split network

Table 11BCVA: mean difference at 12 and 24 months – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	Between-study SD
93.88 (compared to 99 datapoints)	277	198.4	78.67	355.7	0–12 months: 0.534 (95%CI: 0.017, 1.857) 12–24 months: 0.712 (95%CI: 0.094, 1.934)

G.2.1.1.2.1. 12 months

Table 12BCVA: mean difference at 12 months – relative effectiveness of all pairwise combinations

	Rani\|0.5\|1mo	Aflib\|0.5\|1mo	Aflib\|0.5\|Loading --> PRN <6wkly	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Aflib\|2\|Loading --> PRN <6wkly	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|PRN >6wkly	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham anti-VEGF	Sham PDT
Rani\|0.5\|1mo		−0.4 (−2.0, 1.2)	-	0.5 (−1.1, 2.1)	−0.3 (−2.0, 1.3)	-	−1.6 (−3.0, −0.2)	-	-	-	−2.7 (−5.0, −0.5)	−3.0 (−5.0, −1.0)	-	−19.3 (−21.6, −17.0)	−4.6 (−7.3, −1.8)	−2.3 (−3.6, −0.9)	-	−1.8 (−3.7, 0.0)	−1.5 (−3.2, 0.3)	−1.0 (−2.8, 0.8)	−1.5 (−3.2, 0.2)	−19.0 (−22.6, −15.4)	-
Aflib\|0.5\|1mo	−0.5 (−2.7, 1.9)		-	0.9 (−0.6, 2.5)	0.1 (−1.5, 1.7)	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|0.5\|Loading -> PRN <6wkly				-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|2\|1mo	0.5 (−1.7, 2.8)	1.0 (−1.3, 3.1)			−0.8 (−2.4, 0.7)	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|2\|Loading -> 2mo	−0.3 (−2.6, 2.0)	0.1 (−2.2, 2.4)		−0.8 (−3.1, 1.5)		-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|2\|Loading -> PRN <6wkly							-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|1mo	−1.4 (−3.2, 0.4)	−0.9 (−3.9, 1.9)		−1.9 (−4.9, 0.9)	−1.0 (−4.0, 1.8)			4.1 (−0.5, 8.7)	−0.3 (−5.2, 4.6)	-	0.8 (−1.4, 3.0)	−2.3 (−4.2, −0.3)	-	-	-	0.1 (−2.2, 2.3)	-	−1.2 (−3.1, 0.8)	-	-	-	-	-
Beva\|1.25\|2mo	2.8 (−2.5, 8.2)	3.3 (−2.5, 9.1)		2.4 (−3.4, 8.0)	3.1 (−2.6, 9.0)		4.2 (−0.7, 9.6)		−4.4 (−8.1, −0.7)	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|6wk	−1.6 (−7.2, 4.4)	−1.1 (−7.1, 5.3)		−2.1 (−8.1, 4.4)	−1.3 (−7.3, 5.0)		−0.2 (−5.5, 5.7)	−4.4 (−8.5, −0.4)		−2.5 (−7.1, 2.1)	-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|Loadin g -> 12wk	−4.0 (−11.6, 5.0)	−3.5 (−11.4, 5.9)		−4.4 (−12.4, 4.8)	−3.7 (−11.6, 5.7)		−2.6 (−10.0, 5.8)	−6.8 (−13.5, 0.0)	−2.4 (−7.7, 2.7)		-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|Loadin g -> PRN <6wkly	−2.0 (−4.1, 0.1)	−1.5 (−4.7, 1.5)		−2.4 (−5.6, 0.6)	−1.6 (−4.9, 1.4)		−0.6 (−2.9, 1.7)	−4.8 (−10.1, 0.6)	−0.4 (−6.5, 5.3)	2.0 (−7.1, 9.8)		0.3 (−4.1, 4.7)	-	−11.0 (−21.0, −1.0)	-	−0.8 (−2.2, 0.7)	-	-	-	-	-	-	-
Beva\|1.25\|PRN <6wkly	−2.8 (−5.1, −0.5)	−2.3 (−5.6, 0.8)		−3.3 (−6.5, −0.2)	−2.4 (−5.8, 0.7)		−1.4 (−3.7, 1.0)	−5.6 (−11.1, −0.2)	−1.2 (−7.3, 4.7)	1.2 (−7.7, 9.0)	−0.8 (−3.5, 1.9)		-	-	-	-	-	1.2 (−0.6, 3.1)	-	-	-	-	-
Beva\|1.25\|Treat and extend	−1.6 (−5.2, 2.4)	−1.1 (−5.5, 3.3)		−2.0 (−6.4, 2.4)	−1.3 (−5.5, 3.3)		−0.2 (−4.3, 4.3)	−4.4 (−10.8, 2.1)	0.0 (−6.8, 6.8)	2.5 (−6.7, 11.1)	0.4 (−3.8, 4.9)	1.2 (−3.1, 5.9)		-	-	-	-	-	−0.1 (−2.2, 1.9)	-	-	-	-
PDT\|PRN >6wkly	−18.9 (−21.9, −15.5)	−18.4 (−22.3, −14.2)		−19.3 (−23.1, −15.3)	−18.5 (−22.4, −14.4)		−17.5 (−20.9, −13.6)	−21.7 (−27.9, −15.3)	−17.2 (−23.9, −10.6)	−14.8 (−24.0, −6.4)	−16.9 (−20.6, −13.1)	−16.0 (−19.7, −12.0)	−17.3 (−22.1, −12.3)		-	-	-	-	-	-	-	-	−4.3 (−6.2, −2.3)
Rani\|0.5\|Loading -> 3mo	−4.1 (−6.9, −1.1)	−3.7 (−7.3, 0.1)		−4.6 (−8.2, −0.9)	−3.8 (−7.4, −0.1)		−2.8 (−6.1, 0.8)	−6.9 (−13.2, −0.8)	−2.5 (−9.0, 3.8)	−0.1 (−9.1, 8.2)	−2.2 (−5.5, 1.5)	−1.4 (−4.9, 2.5)	−2.6 (−7.5, 2.2)	14.6 (10.4, 19.1)		-	-	-	-	-	-	−15.4 (−21.5, −9.4)	-
Rani\|0.5\|Loading -> PRN <6wkly	−2.2 (−4.0, −0.4)	−1.7 (−4.7, 1.2)		−2.7 (−5.6, 0.2)	−1.8 (−4.8, 1.0)		−0.8 (−3.0, 1.4)	−5.0 (−10.5, 0.4)	−0.6 (−6.6, 5.1)	1.8 (−7.2, 9.6)	−0.2 (−1.9, 1.6)	0.6 (−2.1, 3.3)	−0.7 (−5.0, 3.5)	16.7 (12.9, 20.2)	1.9 (−1.6, 5.3)		4.5 (−3.8, 12.8)	-	-	0.6 (−1.2, 2.4)	0.1 (−1.6, 1.8)	-	-
Rani\|0.5\|Loading -> PRNX	2.0 (−6.4, 11.0)	2.5 (−5.8, 11.6)		1.5 (−7.0, 10.6)	2.3 (−6.1, 11.7)		3.4 (−5.0, 12.4)	−0.8 (−10.8, 9.7)	3.7 (−6.8, 14.0)	6.2 (−5.6, 17.6)	4.0 (−4.2, 13.0)	4.9 (−3.7, 13.9)	3.6 (−6.0, 13.4)	20.8 (11.8, 30.5)	6.2 (−2.5, 15.4)	4.3 (−3.8, 12.9)		-	-	-	-	-	-
Rani\|0.5\|PRN <6wkly	−2.0 (−4.6, 0.5)	−1.5 (−4.9, 1.7)		−2.5 (−5.9, 0.8)	−1.7 (−5.2, 1.6)		−0.6 (−3.3, 1.9)	−4.9 (−10.4, 0.7)	−0.4 (−6.7, 5.6)	1.9 (−7.4, 9.8)	0.0 (−3.2, 2.9)	0.8 (−1.9, 3.4)	−0.4 (−5.2, 3.9)	16.8 (12.6, 20.8)	2.1 (−1.8, 5.8)	0.2 (−2.8, 3.1)	−4.0 (−13.3, 4.5)		-	-	-	-	-
Rani\|0.5\|Treat and extend	−1.3 (−3.5, 1.0)	−0.8 (−4.0, 2.4)		−1.8 (−4.9, 1.5)	−1.0 (−4.0, 2.3)		0.1 (−2.7, 3.1)	−4.2 (−9.7, 1.7)	0.3 (−6.0, 6.3)	2.6 (−6.6, 10.7)	0.7 (−2.3, 3.9)	1.5 (−1.6, 4.8)	0.2 (−2.9, 3.4)	17.6 (13.7, 21.3)	2.8 (−0.7, 6.5)	0.9 (−1.9, 3.9)	−3.3 (−12.4, 5.2)	0.6 (−2.6, 4.3)		-	-	-	-
Rani\|2\|1mo	−1.1 (−3.7, 1.5)	−0.6 (−4.1, 2.9)		−1.6 (−5.0, 1.9)	−0.8 (−4.2, 2.7)		0.3 (−2.7, 3.4)	−3.9 (−9.9, 1.9)	0.5 (−6.1, 6.6)	2.9 (−6.4, 10.9)	0.8 (−2.1, 4.0)	1.7 (−1.8, 5.2)	0.5 (−4.3, 5.0)	17.7 (13.5, 21.8)	3.0 (−0.7, 6.8)	1.1 (−1.5, 3.8)	−3.1 (−12.3, 5.3)	0.9 (−2.6, 4.5)	0.2 (−3.4, 3.6)		−0.5 (−2.3, 1.3)	-	-
Rani\|2\|Loading -> PRN <6wkly	−1.6 (−4.3, 0.9)	−1.2 (−4.7, 2.3)		−2.1 (−5.6, 1.3)	−1.3 (−4.8, 2.2)		−0.3 (−3.2, 2.8)	−4.5 (−10.4, 1.2)	0.0 (−6.7, 6.0)	2.3 (−6.8, 10.5)	0.3 (−2.6, 3.3)	1.2 (−2.2, 4.5)	−0.1 (−4.8, 4.3)	17.2 (13.0, 21.2)	2.6 (−1.4, 6.2)	0.6 (−2.1, 3.1)	−3.6 (−12.7, 5.2)	0.4 (−3.1, 3.9)	−0.4 (−3.9, 3.0)	−0.6 (−3.5, 2.4)		-	-
Sham anti-VEGF	−17.6 (−20.3, −15.0)	−17.1 (−20.7, −13.7)		−18.0 (−21.6, −14.7)	−17.2 (−20.8, −13.8)		−16.2 (−19.4, −13.0)	−20.5 (−26.2, −14.3)	−16.1 (−22.2, −9.7)	−13.7 (−22.8, −5.4)	−15.6 (−19.0, −12.2)	−14.8 (−18.4, −11.3)	−16.1 (−20.7, −11.4)	1.2 (−3.1, 5.3)	−13.5 (−17.1, −10.1)	−15.4 (−18.6, −12.2)	−19.7 (−28.8, −10.9)	−15.6 (−19.3, −11.9)	−16.2 (−19.9, −12.8)	−16.4 (−20.2, −12.8)	−16.0 (−19.6, −12.2)		-
Sham PDT	−23.5 (−27.5, −19.4)	−23.0 (−27.6, −18.4)		−24.0 (−28.4, −19.3)	−23.2 (−27.8, −18.5)		−22.2 (−26.3, −17.7)	−26.4 (−33.0, −19.5)	−21.9 (−29.2, −14.9)	−19.5 (−29.0, −10.6)	−21.6 (−25.8, −17.1)	−20.7 (−25.1, −16.1)	−22.0 (−27.3, −16.5)	−4.7 (−7.1, −2.4)	−19.3 (−24.4, −14.5)	−21.4 (−25.5, −17.0)	−25.5 (−35.6, −16.3)	−21.5 (−26.1, −16.7)	−22.1 (−26.6, −17.7)	−22.4 (−27.1, −17.7)	−21.9 (−26.4, −17.0)	−5.9 (−10.7, −1.1)

: Values given are mean differences. The segment below and to the left of the shaded cells is derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects (row versus column). The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals. The segment above and to the right of the shaded cells gives pooled direct evidence (random-effects pairwise meta-analysis), where available (column versus row). Numbers in parentheses are 95% confidence intervals.

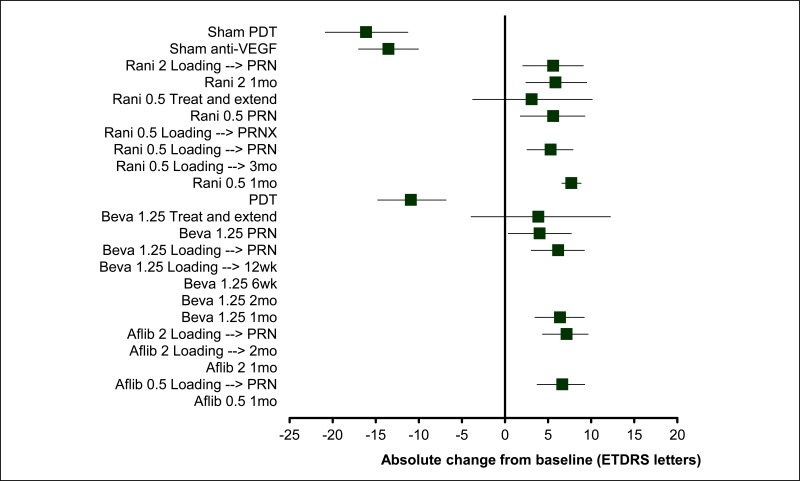
Figure 9BCVA: mean difference at 12 months – relative effect of all options versus monthly ranibizumab 0.5mg

Values less than 0 favour ranibizumab 0.5mg 1mo; values greater than 0 favour the comparator treatment. Solid error bars are 95% credible intervals; dashed error bars are 95% confidence interval.

Figure 10BCVA: mean difference at 12 months – expected absolute change

Table 13BCVA: mean difference at 12 months – rankings for each comparator

	Probability best	Median rank (95%CI)
Aflib 0.5 1mo	0.008	7 (2, 15)
Aflib 2 1mo	0.061	4 (1, 11)
Aflib 2 Loading -> 2mo	0.013	6 (2, 15)
Beva 1.25 1mo	0.000	10 (4, 15)
Beva 1.25 2mo	0.455	2 (1, 12)
Beva 1.25 6wk	0.004	11 (2, 17)
Beva 1.25 Loading -> 12wk	0.016	17 (2, 18)
Beva 1.25 Loading -> PRN	0.000	12 (5, 17)
Beva 1.25 PRN	0.000	15 (7, 18)
Beva 1.25 Treat and extend	0.020	10 (2, 18)
PDT	0.000	20 (19, 20)
Rani 0.5 1mo	0.006	5 (2, 9)
Rani 0.5 Loading -> 3mo	0.000	17 (8, 18)
Rani 0.5 Loading -> PRN	0.000	13 (7, 17)
Rani 0.5 Loading -> PRNX	0.402	2 (1, 18)
Rani 0.5 PRN	0.002	12 (4, 17)
Rani 0.5 Treat and extend	0.003	10 (3, 16)
Rani 2 1mo	0.009	9 (2, 16)
Rani 2 Loading -> PRN	0.002	11 (3, 17)
Sham anti-VEGF	0.000	19 (19, 20)
Sham PDT	0.000	21 (21, 21)

Figure 11BCVA: mean difference at 12 months – rank probability histograms

G.2.1.1.2.2. 24 months

Table 14BCVA: mean difference at 24 months – relative effectiveness of all pairwise combinations

	Rani\|0.5\|1mo	Aflib\|0.5\|1mo	Aflib\|0.5\|Loading --> PRN <6wkly	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Aflib\|2\|Loading --> PRN <6wkly	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|PRN >6wkly	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham anti-VEGF	Sham PDT
Rani\|0.5\|1mo		-	-	-	-	-	−2.4 (−5.0, 0.3)	-	-	-	−2.8 (−6.1, 0.5)	−3.8 (−7.3, −0.3)	-	−19.2 (−22.7, −15.7)	-	−2.7 (−6.1, 0.7)	-	−2.1 (−5.3, 1.1)	−1.8 (−9.8, 6.2)	−1.1 (−3.8, 1.6)	−1.5 (−4.0, 1.0)	−20.9 (−23.7, −18.1)	-
Aflib\|0.5\|1mo			-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|0.5\|Loading -> PRN <6wkly	−1.0 (−3.9, 1.3)			-	-	1.0 (−0.5, 2.5)	-	-	-	-	-	-	-	-	-	1.3 (−0.5, 3.1)	-	-	-	-	-	-	-
Aflib\|2\|1mo					-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|2\|Loading -> 2mo						-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Aflib\|2\|Loading -> PRN <6wkly	−0.5 (−3.1, 1.7)		0.5 (−1.3, 2.3)				-	-	-	-	-	-	-	-	-	0.3 (−1.3, 1.8)	-	-	-	-	-	-	-
Beva\|1.25\|1mo	−1.3 (−4.0, 1.3)		−0.3 (−3.6, 3.4)			−0.8 (−4.1, 2.7)		-	-	-	0.9 (−2.4, 4.2)	−2.8 (−6.3, 0.7)	-	-	-	−1.0 (−4.6, 2.6)	-	−1.1 (−4.3, 2.1)	-	-	-	-	-
Beva\|1.25\|2mo									-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|6wk										-	-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|Loading -> 12wk											-	-	-	-	-	-	-	-	-	-	-	-	-
Beva\|1.25\|Loading -> PRN <6wkly	−1.5 (−4.5, 1.3)		−0.5 (−4.1, 3.2)			−1.0 (−4.5, 2.6)	−0.2 (−3.5, 3.0)					-	-	-	-	−1.9 (−5.1, 1.3)	-	-	-	-	-	-	-
Beva\|1.25\|PRN <6wkly	−3.7 (−7.3, −0.2)		−2.6 (−6.8, 1.8)			−3.1 (−7.3, 1.2)	−2.4 (−5.9, 1.1)				−2.2 (−6.2, 2.0)		-	-	-	-	-	1.7 (−1.1, 4.5)	-	-	-	-	-
Beva\|1.25\|Treat and extend	−3.8 (−11.6, 4.5)		−2.7 (−10.9, 5.9)			−3.2 (−11.3, 5.4)	−2.5 (−10.7, 6.3)				−2.3 (−10.6, 6.6)	−0.1 (−8.9, 9.1)		-	-	-	-	-	−0.8 (−4.1, 2.5)	-	-	-	-
PDT\|PRN >6wkly	−18.6 (−22.4, −14.7)		−17.6 (−22.0, −12.9)			−18.1 (−22.3, −13.5)	−17.3 (−21.9, −12.6)				−17.1 (−21.7, −12.4)	−14.9 (−20.0, −9.8)	−14.8 (−23.8, −6.0)		-	-	-	-	-	-	-	-	−3.0 (−6.9, 1.0)
Rani\|0.5\|Loading -> 3mo																-	-	-	-	-	-	-	-
Rani\|0.5\|Loading -> PRN <6wkly	−2.4 (−5.0, −0.1)		−1.3 (−4.1, 1.4)			−1.9 (−4.5, 0.6)	−1.1 (−4.4, 2.0)				−0.9 (−3.8, 1.8)	1.3 (−2.9, 5.3)	1.4 (−7.3, 9.6)	16.2 (11.6, 20.6)			-	-	-	0.1 (−2.6, 2.8)	−0.3 (−2.8, 2.2)	-	-
Rani\|0.5\|Loading -> PRNX																		-	-	-	-	-	-
Rani\|0.5\|PRN <6wkly	−2.1 (−5.8, 1.4)		−1.0 (−5.3, 3.3)			−1.5 (−5.8, 2.8)	−0.8 (−4.4, 2.8)				−0.6 (−4.9, 3.6)	1.6 (−2.0, 5.1)	1.7 (−7.4, 10.4)	16.5 (11.2, 21.7)		0.3 (−3.9, 4.5)			-	-	-	-	-
Rani\|0.5\|Treat and extend	−4.6 (−11.4, 2.4)		−3.5 (−10.7, 3.9)			−4.0 (−11.1, 3.3)	−3.3 (−10.5, 4.3)				−3.1 (−10.6, 4.5)	−0.9 (−8.6, 7.0)	−0.9 (−4.9, 3.2)	14.0 (6.2, 21.9)		−2.1 (−9.4, 5.3)		−2.6 (−10.1, 5.6)		-	-	-	-
Rani\|2\|1mo	−1.8 (−5.1, 1.6)		−0.7 (−4.6, 3.2)			−1.3 (−4.9, 2.7)	−0.5 (−4.7, 3.7)				−0.3 (−4.4, 3.9)	1.9 (−3.0, 6.8)	2.0 (−6.9, 10.6)	16.8 (11.7, 22.0)		0.6 (−2.6, 4.2)		0.3 (−4.6, 5.4)	2.8 (−4.8, 10.5)		−0.4 (−3.1, 2.3)	-	-
Rani\|2\|Loading -> PRN <6wkly	−2.1 (−5.5, 1.2)		−1.0 (−4.9, 2.8)			−1.6 (−5.3, 2.2)	−0.8 (−4.9, 3.3)				−0.6 (−4.7, 3.4)	1.6 (−3.1, 6.4)	1.7 (−7.1, 10.0)	16.5 (11.5, 21.5)		0.3 (−2.9, 3.7)		0.0 (−4.8, 4.7)	2.4 (−5.2, 10.2)	−0.3 (−4.1, 3.4)		-	-
Sham anti-VEGF	−21.3 (−24.6, −17.9)		−20.2 (−24.3, −15.8)			−20.7 (−24.7, −16.4)	−19.9 (−24.3, −15.7)				−19.7 (−24.2, −15.2)	−17.6 (−22.4, −12.6)	−17.5 (−26.3, −8.8)	−2.6 (−7.7, 2.4)		−18.8 (−22.9, −14.6)		−19.1 (−24.0, −14.3)	−16.6 (−24.4, −8.9)	−19.4 (−24.2, −14.7)	−19.1 (−23.7, −14.4)		-
Sham PDT	−23.8 (−28.5, −19.1)		−22.7 (−27.9, −17.3)			−23.3 (−28.3, −17.8)	−22.5 (−27.8, −17.1)				−22.3 (−27.5, −16.8)	−20.1 (−25.8, −14.3)	−20.0 (−29.3, −10.7)	−5.2 (−7.9, −2.6)		−21.4 (−26.5, −16.0)		−21.8 (−27.5, −15.7)	−19.2 (−27.4, −11.0)	−22.0 (−27.8, −16.2)	−21.7 (−27.4, −15.9)	−2.6 (−8.5, 3.2)

: Values given are mean differences. The segment below and to the left of the shaded cells is derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects (row versus column). The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals. The segment above and to the right of the shaded cells gives pooled direct evidence (random-effects pairwise meta-analysis), where available (column versus row). Numbers in parentheses are 95% confidence intervals.

Figure 12BCVA: mean difference at 24 months – relative effect of all options versus reference treatment

Values less than 0 favour ranibizumab 0.5mg 1mo; values greater than 0 favour the comparator treatment. Solid error bars are 95% credible intervals; dashed error bars are 95% confidence interval.

Figure 13BCVA: mean difference at 24 months – expected absolute change

Table 15BCVA: mean difference at 24 months – rankings for each comparator

	Probability best	Median rank (95%CI)
Aflib 0.5 Loading -> PRN	0.045	5 (1, 10)
Aflib 2 Loading -> PRN	0.152	3 (1, 9)
Beva 1.25 1mo	0.074	5 (1, 10)
Beva 1.25 Loading -> PRN	0.061	6 (1, 11)
Beva 1.25 PRN	0.005	10 (3, 12)
Beva 1.25 Treat and extend	0.133	10 (1, 12)
PDT	0.000	13 (13, 14)
Rani 0.5 1mo	0.330	2 (1, 6)
Rani 0.5 Loading -> PRN	0.002	8 (4, 12)
Rani 0.5 PRN	0.059	7 (1, 12)
Rani 0.5 Treat and extend	0.025	11 (1, 12)
Rani 2 1mo	0.072	7 (1, 12)
Rani 2 Loading -> PRN	0.041	7 (1, 12)
Sham anti-VEGF	0.000	14 (13, 15)
Sham PDT	0.000	15 (14, 15)

Figure 14BCVA: mean difference at 24 months – rank probability histograms

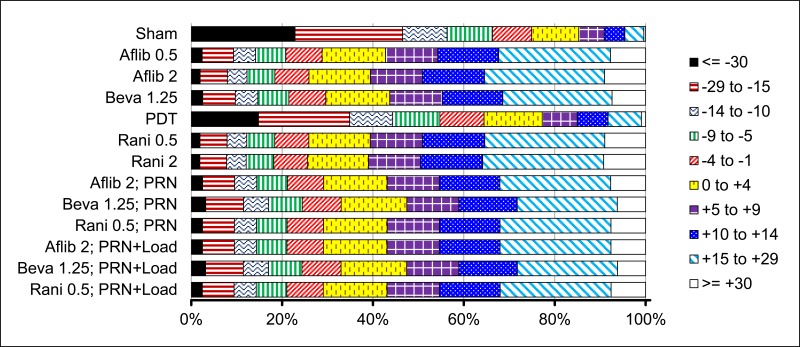
G.2.1.2. Categorical (5-category)

G.2.1.2.1. Model selection

Model fit statistics for 12- and 24-month 5-category NMAs are shown in Table 16.

As noted in G.1.1.4, once we had selected the optimal model for the most critical NMA (bivariate normal mean difference at 12 and 24 months; see G.2.1.1.1.1), model selection for other outcomes sought to disprove that this was the globally optimal model, rather than to establish what could be argued to be best for that particular outcome. In this instance, it was clear that the preferred (random-effects, MR4c) approach was better than fixed and/or unadjusted models at 12 months, so we were happy to use the same approach for this outcome.

For the 24-month synthesis, no data are available for TREX, PRNX or frequencies of routine administration other than monthly (see G.2.1.1). Therefore, in this outcome (for which separate analyses must be performed for the 2 timepoints), it is not possible to adjust for these features in the 2-year analysis. Nevertheless a random-effects model that adjusted for PRN and pre-PRN loading was seen to improve model fit compared with fixed-effects and/or unadjusted approaches, so it was preferred.

Table 16BCVA: categorical (5-category) at 12 and 24 months – summary model fit statistics, showing selection of best-fitting models

Outcome	Model for treatment differences	Number of discrete nodes	Model for category differences	Covariates					N	Total residual deviance	DIC	Standard deviation of random effects distributions (95%CrI)
Outcome	Model for treatment differences	Number of discrete nodes	Model for category differences	PRN	Loading	TREX	PRNX	Frequency	N	Total residual deviance	DIC	Between treatments	Between categories
Categorical change in BCVA at 12mo (5-category split)	FIXED	20	FIXED						149	216.8	831.6	n/a	n/a
	FIXED		RANDOM							174.2	806.3	n/a	0.16 (0.09, 0.26)
	RANDOM		FIXED							211.8	831.8	0.08 (0.004, 0.20)	n/a
	RANDOM		RANDOM							170.4	807.1	0.07 (0.005, 0.19)	0.16 (0.09, 0.27)
	RANDOM MR4c	7	FIXED	✓	✓	✓	✓	✓		211.2	824.5	0.07 (0.01, 0.16)	n/a
	RANDOM MR4c	7	RANDOM	✓	✓	✓	✓	✓		172.2	801.4	0.06 (0.004, 0.15)	0.15 (0.08, 0.25)
Categorical change in BCVA at 24mo (5-category split)	FIXED	12	FIXED						94	169.1	613.4	n/a	n/a
	FIXED		RANDOM							105.3	563.5	n/a	0.18 (0.11, 0.30)
	RANDOM		FIXED							166.1	614.5	0.08 (0.004, 0.24)	n/a
	RANDOM		RANDOM							102.7	564.8	0.07 (0.004, 0.23)	0.18 (0.11, 0.30)
	RANDOM MR2	7	FIXED	✓	✓	n/a	n/a	n/a		165.2	610.4	0.06 (0.006, 0.18)	n/a
	RANDOM MR2	7	RANDOM	✓	✓	n/a	n/a	n/a		102.0	560.7	0.06 (0.004, 0.17)	0.11 (0.07, 0.17)

: MR4a = 1 covariate shared between anti-VEGF agents for frequency–response effect; MR4b = separate covariates for each anti-VEGF agent for frequency–response effect; MR4c = 1 covariate for aflibercept and 1 covariate for bevacizumab and ranibizuamb for frequency–response effect;

G.2.1.2.2. Categorical change at 1 year (5-category; RE; meta-regression)

Table 17BCVA: categorical change at 1 year (5-category; RE; meta-regression) – input data

Study	Change in ETDRS letters		Aflib\|0.5\|1mo	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
Study	Minimum	Maximum	Aflib\|0.5\|1mo	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
ANCHOR 2006		−30											19	0
	−29	−15											32	14
	−14	+14											84	160
	+15	+29											8	80
	+30												0	26
Barikian 2015		−15								0	0
	−14	+14								18	20
	+15									12	10
BRAMD 2016		−15				18								8
	−14	+14				104								126
	+15					39								32
CATT 2011		−15				16					23			16				13
	−14	+14				166					172			171				201
	+15					83					76			97				71
El-Mollayess		+14				39					36
El-Mollayess	+15					21					24
EXCITE 2010		−30												0	4
	−29	−15												6	14
	−14	+14												76	182
	+15													33	38
GEFAL 2013		−15								17						18
	−14	+14								135						126
	+15									39						39
HARBOR		−15												6		15				18	14
	−14	+14												174		177				157	169
	+15													95		83				99	90
IVAN 2013		−30				2				1				3		0
	−29	−15				5				4				3		6
	−14	+14				108				106				98		108
	+15	+29				14				22				26		26
	+30					5				3				10		3
LUCAS 2015		−15										7							8
	−14	+14										130							129
	+15											47							50
Lushchyk 2013		−15				3	0	6
	−14	+14				37	47	43
	+15					6	7	8
MANTA 2013		−15								8						10
	−14	+14								110						118
	+15									36						35
MARINA		−15												26								90
	−14	+14												312								136
	+15													140								12
NATTB 2013		−15						3	5
	−14	+14						41	44
	+15							35	33
PIER		−15													16							32
	−14	+14													89							25
	+15														15							6
Sacu 2009		−15								0			2
	−14	+14								10			11
	+15									4			1
SALUTE 2015		−30														2	1
	−29	−15														2	3
	−14	+14														26	21
	+15															9	13
Subramanian 2010		−30								0						0
	−29	−15								0						1
	−14	−5								10						5
	+15	+29								3						0
	+30									2						1
TAP 1999		−30											59									49
	−29	−15											97									62
	−14	+14											222									91
	+15	+29											20									5
	+30												4									0
TREX 2015		+14												17					30
TREX 2015	+15													3					10
VIEW 1&2 POOLED		−15	29	32	31									34
	−14	+14	390	376	388									368
	+15		178	205	188									193
VIM 2005		−30											3									6
	−29	−15											7									12
	−14	+14											25									20
	+15												1									0
VIP 2001 Occ only		−30											37									30
	−29	−15											48									21
	−14	+14											76									39
	+15	+29											5									2
VIO		−30											39									20
	−29	−15											51									34
	−14												154									66

: Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

Table 18BCVA: categorical change at 1 year (5-category; RE; meta-regression) – relative effectiveness of all pairwise combinations

Sham

−1.31 (−1.57, −1.04)

Aflib 0.5

−1.42 (−1.81, −1.03)

−0.12 (−0.45, 0.24)

Aflib 2

−1.48 (−1.72, −1.23)

−0.17 (−0.42, 0.08)

−0.05 (−0.42, 0.31)

Beva 1.25

−0.22 (−0.36, −0.08)

1.09 (0.81, 1.37)

1.20 (0.81, 1.60)

1.26 (1.01, 1.51)

PDT

−1.51 (−1.73, −1.29)

−0.20 (−0.43, 0.02)

−0.09 (−0.44, 0.26)

−0.03 (−0.13, 0.07)

−1.29 (−1.52, −1.06)

Rani 0.5

−1.34 (−1.59, −1.09)

−0.03 (−0.30, 0.23)

0.08 (−0.31, 0.45)

0.13 (−0.10, 0.38)

−1.12 (−1.39, −0.87)

0.17 (−0.04, 0.38)

Rani 2

−1.32 (−1.75, −0.90)

−0.02 (−0.38, 0.36)

0.10 (−0.04, 0.24)

0.15 (−0.24, 0.56)

−1.10 (−1.52, −0.69)

0.19 (−0.19, 0.57)

0.02 (−0.38, 0.43)

Aflib 2 PRN

−1.38 (−1.66, −1.10)

−0.07 (−0.35, 0.20)

0.05 (−0.35, 0.43)

0.10 (−0.04, 0.24)

−1.16 (−1.45, −0.87)

0.13 (−0.03, 0.29)

−0.03 (−0.30, 0.22)

−0.05 (−0.42, 0.31)

Beva 1.25 PRN

−1.41 (−1.68, −1.14)

−0.10 (−0.37, 0.16)

0.02 (−0.38, 0.38)

0.07 (−0.12, 0.26)

−1.19 (−1.47, −0.92)

0.10 (−0.04, 0.24)

−0.07 (−0.33, 0.18)

−0.09 (−0.44, 0.26)

−0.03 (−0.13, 0.07)

Rani 0.5 PRN

−1.34 (−1.75, −0.93)

−0.03 (−0.39, 0.35)

0.09 (−0.04, 0.21)

0.14 (−0.25, 0.54)

−1.11 (−1.53, −0.71)

0.17 (−0.20, 0.56)

0.00 (−0.39, 0.41)

−0.01 (−0.19, 0.16)

0.04 (−0.36, 0.46)

0.07 (−0.32, 0.48)

Aflib 2 PRNL

−1.39 (−1.67, −1.12)

−0.09 (−0.36, 0.19)

0.03 (−0.36, 0.41)

0.09 (−0.04, 0.21)

−1.17 (−1.45, −0.90)

0.12 (−0.04, 0.28)

−0.05 (−0.32, 0.21)

−0.07 (−0.49, 0.34)

−0.01 (−0.19, 0.16)

0.02 (−0.20, 0.23)

−0.05 (−0.42, 0.31)

Beva 1.25 PRNL

−1.42 (−1.68, −1.17)

−0.12 (−0.38, 0.15)

0.00 (−0.38, 0.37)

0.06 (−0.11, 0.22)

−1.20 (−1.46, −0.95)

0.09 (−0.04, 0.21)

−0.08 (−0.33, 0.17)

−0.10 (−0.50, 0.29)

−0.04 (−0.25, 0.15)

−0.01 (−0.19, 0.16)

−0.09 (−0.44, 0.26)

−0.03 (−0.13, 0.07)

Rani 0.5 PRNL

−1.81 (−2.74, −0.93)

−0.50 (−1.42, 0.35)

−0.39 (−1.24, 0.41)

−0.33 (−1.27, 0.55)

−1.59 (−2.52, −0.70)

−0.30 (−1.22, 0.57)

−0.47 (−1.40, 0.41)

−0.49 (−1.35, 0.32)

−0.43 (−1.37, 0.45)

−0.39 (−1.33, 0.48)

−0.47 (−1.33, 0.34)

−0.41 (−1.35, 0.47)

−0.38 (−1.32, 0.49)

Aflib 2 TREX

−1.86 (−2.76, −1.04)

−0.56 (−1.45, 0.29)

−0.44 (−1.34, 0.47)

−0.39 (−1.24, 0.41)

−1.64 (−2.53, −0.80)

−0.35 (−1.21, 0.45)

−0.52 (−1.41, 0.31)

−0.54 (−1.46, 0.38)

−0.49 (−1.35, 0.32)

−0.45 (−1.33, 0.36)

−0.53 (−1.44, 0.39)

−0.47 (−1.33, 0.34)

−0.44 (−1.30, 0.37)

−0.05 (−0.42, 0.31)

Beva 1.25 TREX

−1.89 (−2.79, −1.06)

−0.59 (−1.48, 0.25)

−0.47 (−1.37, 0.43)

−0.42 (−1.27, 0.38)

−1.67 (−2.56, −0.84)

−0.39 (−1.24, 0.41)

−0.55 (−1.43, 0.27)

−0.57 (−1.48, 0.34)

−0.52 (−1.38, 0.30)

−0.49 (−1.35, 0.32)

−0.56 (−1.47, 0.34)

−0.50 (−1.37, 0.30)

−0.47 (−1.33, 0.34)

−0.09 (−0.44, 0.26)

−0.03 (−0.13, 0.07)

Rani 0.5 TREX

−1.59 (−2.25, −0.92)

−0.29 (−0.93, 0.36)

−0.17 (−0.72, 0.40)

−0.12 (−0.76, 0.55)

−1.37 (−2.03, −0.70)

−0.08 (−0.73, 0.57)

−0.25 (−0.91, 0.41)

−0.27 (−0.84, 0.31)

−0.21 (−0.87, 0.46)

−0.18 (−0.83, 0.49)

−0.26 (−0.79, 0.29)

−0.20 (−0.83, 0.47)

−0.17 (−0.80, 0.49)

0.22 (−0.76, 1.23)

0.28 (−0.79, 1.35)

0.31 (−0.74, 1.38)

Aflib 2 PRNX

−1.65 (−2.24, −1.03)

−0.34 (−0.95, 0.27)

−0.22 (−0.89, 0.44)

−0.17 (−0.72, 0.40)

−1.43 (−2.03, −0.81)

−0.14 (−0.69, 0.43)

−0.31 (−0.90, 0.30)

−0.32 (−1.01, 0.37)

−0.27 (−0.84, 0.31)

−0.24 (−0.81, 0.35)

−0.31 (−0.97, 0.36)

−0.26 (−0.79, 0.29)

−0.22 (−0.76, 0.33)

0.16 (−0.90, 1.23)

0.22 (−0.76, 1.23)

0.25 (−0.73, 1.27)

−0.05 (−0.42, 0.31)

Beva 1.25 PRNX

−1.68 (−2.27, −1.08)

−0.37 (−0.97, 0.23)

−0.26 (−0.92, 0.40)

−0.20 (−0.77, 0.37)

−1.46 (−2.05, −0.85)

−0.17 (−0.72, 0.40)

−0.34 (−0.93, 0.26)

−0.35 (−1.03, 0.32)

−0.30 (−0.87, 0.28)

−0.27 (−0.84, 0.31)

−0.34 (−0.99, 0.31)

−0.29 (−0.84, 0.27)

−0.26 (−0.79, 0.29)

0.13 (−0.92, 1.20)

0.19 (−0.81, 1.20)

0.22 (−0.76, 1.23)

−0.09 (−0.44, 0.26)

−0.03 (−0.13, 0.07)

Rani 0.5 PRNX

−1.38 (−1.64, −1.11)

−0.07 (−0.27, 0.13)

0.05 (−0.15, 0.24)

0.10 (−0.14, 0.35)

−1.15 (−1.43, −0.88)

0.14 (−0.09, 0.36)

−0.03 (−0.29, 0.23)

−0.05 (−0.29, 0.19)

0.00 (−0.27, 0.28)

0.04 (−0.22, 0.30)

−0.04 (−0.28, 0.20)

0.02 (−0.26, 0.29)

0.05 (−0.21, 0.31)

0.44 (−0.38, 1.31)

0.49 (−0.36, 1.36)

0.52 (−0.32, 1.39)

0.22 (−0.38, 0.79)

0.27 (−0.35, 0.89)

0.30 (−0.30, 0.91)

Aflib 2 2mo

−1.31 (−1.51, −1.11)

−0.01 (−0.23, 0.22)

0.12 (−0.25, 0.47)

0.17 (0.06, 0.27)

−1.09 (−1.30, −0.87)

0.20 (0.05, 0.35)

0.03 (−0.18, 0.23)

0.01 (−0.39, 0.40)

0.07 (−0.11, 0.25)

0.10 (−0.11, 0.32)

0.03 (−0.36, 0.41)

0.08 (−0.09, 0.25)

0.11 (−0.08, 0.31)

0.50 (−0.39, 1.43)

0.55 (−0.25, 1.42)

0.59 (−0.22, 1.45)

0.28 (−0.37, 0.92)

0.34 (−0.24, 0.90)

0.37 (−0.21, 0.94)

0.06 (−0.16, 0.29)

Beva 1.25 2mo

−1.34 (−1.52, −1.17)

−0.04 (−0.23, 0.17)

0.08 (−0.27, 0.42)

0.14 (−0.01, 0.28)

−1.12 (−1.31, −0.94)

0.17 (0.06, 0.27)

0.00 (−0.18, 0.18)

−0.02 (−0.40, 0.35)

0.04 (−0.16, 0.23)

0.07 (−0.11, 0.25)

−0.01 (−0.38, 0.36)

0.05 (−0.14, 0.24)

0.08 (−0.09, 0.25)

0.47 (−0.41, 1.39)

0.52 (−0.29, 1.39)

0.55 (−0.25, 1.42)

0.25 (−0.40, 0.88)

0.30 (−0.27, 0.87)

0.34 (−0.24, 0.90)

0.03 (−0.17, 0.24)

−0.03 (−0.13, 0.07)

Rani 0.5 2mo

−1.33 (−1.59, −1.07)

−0.02 (−0.22, 0.17)

0.10 (−0.31, 0.48)

0.15 (−0.10, 0.40)

−1.11 (−1.39, −0.83)

0.18 (−0.05, 0.41)

0.01 (−0.25, 0.28)

0.00 (−0.43, 0.41)

0.05 (−0.22, 0.33)

0.08 (−0.19, 0.35)

0.01 (−0.42, 0.42)

0.07 (−0.22, 0.34)

0.10 (−0.17, 0.36)

0.48 (−0.40, 1.42)

0.54 (−0.31, 1.43)

0.57 (−0.26, 1.46)

0.26 (−0.41, 0.93)

0.32 (−0.29, 0.92)

0.35 (−0.26, 0.95)

0.05 (−0.15, 0.24)

−0.02 (−0.24, 0.21)

0.02 (−0.18, 0.21)

Aflib 2 3mo

−1.14 (−1.35, −0.93)

0.16 (−0.09, 0.42)

0.28 (−0.10, 0.65)

0.33 (0.11, 0.55)

−0.92 (−1.14, −0.70)

0.37 (0.13, 0.60)

0.20 (−0.03, 0.42)

0.18 (−0.24, 0.59)

0.23 (−0.02, 0.50)

0.27 (−0.01, 0.55)

0.19 (−0.22, 0.59)

0.25 (−0.01, 0.50)

0.28 (0.01, 0.56)

0.66 (−0.22, 1.60)

0.72 (−0.11, 1.61)

0.75 (−0.09, 1.64)

0.45 (−0.21, 1.11)

0.50 (−0.10, 1.10)

0.54 (−0.07, 1.14)

0.23 (−0.02, 0.48)

0.17 (0.06, 0.27)

0.20 (0.05, 0.35)

0.18 (−0.06, 0.44)

Beva 1.25 3mo

−1.18 (−1.36, −0.99)

0.13 (−0.10, 0.37)

0.25 (−0.12, 0.61)

0.30 (0.06, 0.54)

−0.95 (−1.15, −0.75)

0.33 (0.11, 0.55)

0.17 (−0.04, 0.37)

0.15 (−0.25, 0.54)

0.20 (−0.07, 0.48)

0.23 (−0.02, 0.50)

0.16 (−0.23, 0.55)

0.22 (−0.06, 0.49)

0.25 (−0.01, 0.50)

0.63 (−0.24, 1.56)

0.69 (−0.15, 1.58)

0.72 (−0.11, 1.61)

0.42 (−0.24, 1.06)

0.47 (−0.14, 1.07)

0.50 (−0.10, 1.10)

0.20 (−0.03, 0.43)

0.14 (−0.01, 0.28)

0.17 (0.06, 0.27)

0.15 (−0.07, 0.38)

−0.03 (−0.13, 0.07)

Rani 0.5 3mo

: Values given are z-scores (option on the right versus option above, with negative numbers favouring the option on the right)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

Figure 15BCVA: categorical change at 1 year (5-category; RE; meta-regression) – relative effect of all options versus sham

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 16BCVA: categorical change at 1 year (5-category; RE; meta-regression) – expected proportion of people in each category

Table 19BCVA: categorical change at 1 year (5-category; RE; meta-regression) – 2 meta-regression coefficients

Covariate		Beta	(95%CrI)
PRN		0.10	(−0.04, 0.24)
Loading		−0.01	(−0.19, 0.16)
TREX		−0.39	(−1.24, 0.41)
PRNX		−0.25	(−0.79, 0.29)
Frequency (per additional month)	Aflibercept	0.05	(−0.15, 0.24)
Frequency (per additional month)	Bevacizumab / ranibizumab	0.17	(0.06, 0.27)

: Values on probit scale (z-scores); positive values indicate worse BCVA

Table 20BCVA: categorical change at 1 year (5-category; RE; meta-regression) – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	25 (25, 25)
Aflib 0.5	0.001	17 (7, 23)
Aflib 2	0.014	10 (2, 21)
Beva 1.25	0.008	8 (3, 15)
PDT	0.000	24 (24, 24)
Rani 0.5	0.021	7 (2, 12)
Rani 2	0.002	15 (5, 22)
Aflib 2; PRN	0.001	17 (4, 23)
Beva 1.25; PRN	0.000	13 (6, 22)
Rani 0.5; PRN	0.002	11 (4, 20)
Aflib 2; PRN+Load	0.001	16 (4, 23)
Beva 1.25; PRN+Load	0.000	12 (6, 21)
Rani 0.5; PRN+Load	0.002	10 (4, 19)
Aflib 2; TREX	0.186	3 (1, 23)
Beva 1.25; TREX	0.127	3 (1, 22)
Rani 0.5; TREX	0.329	2 (1, 21)
Aflib 2; PRNX	0.091	6 (1, 23)
Beva 1.25; PRNX	0.057	5 (1, 22)
Rani 0.5; PRNX	0.155	4 (1, 21)
Aflib 2; 2mo	0.000	13 (6, 19)
Beva 1.25; 2mo	0.000	17 (9, 21)
Rani 0.5; 2mo	0.000	15 (8, 20)
Aflib 2; 3mo	0.002	16 (5, 22)
Beva 1.25; 3mo	0.000	22 (16, 23)
Rani 0.5; 3mo	0.000	22 (15, 23)

Figure 17BCVA: categorical change at 1 year (5-category; RE; meta-regression) – rank probability histograms

Table 21BCVA: categorical change at 1 year (5-category; RE; meta-regression) – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	Between-study SD
171.3 (compared to 149 datapoints)	740.3	679.7	60.58	800.9	0.06 (95%CI: 0.00, 0.15)

G.2.1.2.3. Categorical change at 2 years (5-category; RE; meta-regression)

Table 22BCVA: categorical change at 2 years (5-category; RE; meta-regression) – input data

Study	Change in ETDRS letters		Aflib\|0.5\|Loading --> PRN <6wkly	Aflib\|2\|Loading --> PRN <6wkly	Beva\|1.25\|1mo	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|PRN <6wkly	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
Study	Minimum	Maximum	Aflib\|0.5\|Loading --> PRN <6wkly	Aflib\|2\|Loading --> PRN <6wkly	Beva\|1.25\|1mo	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|PRN <6wkly	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
ANCHOR 2006		−30						23	2
	−29	−15						26	29
	−14	+14						85	144
	+15	+29						6	73
	+30							3	32
CATT 2011		−15			10		29		9		19
	−14	+14			78		151		81		164
	+15				41		71		44		81
HARBOR		−15							16	25		27	23
	−14	+14							164	159		144	155
	+15								95	91		103	95
IVAN 2013		−30			4	0			4	4
	−29	−15			8	11			4	11
	−14	+14			90	95			84	98
	+15	+29			19	15			32	18
	+30				5	2			9	4
MARINA		−15							43					112
	−14	+14							293					117
	+15								142					9
TAP 1999		−30						73						62
	−29	−15						116						67
	−14	+14						177						70
	+15	+29						33						8
	+30							3						0
VIEW 1&2 POOLED		−30	▬^a	▬^a						▬^a
	−29	−15	▬^a	▬^a						▬^a
	−14	+14	▬^a	▬^a						▬^a
	+15	+29	▬^a	▬^a						▬^a
	+30		▬^a	▬^a						▬^a
VIM 2005		−30						4						13
	−29	−15						13						10
	−14	+14						12						13
	+15							3						1
VIO		−30						56						30
	−29	−15						59						34
	−14							129						56
VIP 2001 Occ only		−30						48						43
	−29	−15						43						20
	−14	+14						67						28
	+15	+29						8						1
VIP 2001 PC or MC		−30						19						11
	−29	−15						11						2
	−14							29						9

: Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

Table 23BCVA: categorical change at 2 years (5-category; RE; meta-regression) – relative effectiveness of all pairwise combinations

Sham

−1.23 (−1.51, −0.95)

Aflib 0.5

−1.32 (−1.58, −1.06)

−0.09 (−0.27, 0.08)

Aflib 2

−1.17 (−1.42, −0.93)

0.05 (−0.20, 0.30)

0.14 (−0.09, 0.38)

Beva 1.25

−0.33 (−0.47, −0.19)

0.90 (0.62, 1.18)

0.99 (0.73, 1.25)

0.85 (0.60, 1.10)

PDT

−1.30 (−1.49, −1.11)

−0.07 (−0.28, 0.14)

0.02 (−0.16, 0.20)

−0.12 (−0.27, 0.03)

−0.97 (−1.17, −0.77)

Rani 0.5

−1.31 (−1.57, −1.05)

−0.08 (−0.35, 0.19)

0.01 (−0.24, 0.26)

−0.14 (−0.37, 0.10)

−0.98 (−1.24, −0.72)

−0.01 (−0.19, 0.17)

Rani 2

−1.22 (−1.56, −0.90)

0.01 (−0.27, 0.28)

0.10 (−0.11, 0.30)

−0.05 (−0.36, 0.26)

−0.89 (−1.23, −0.57)

0.07 (−0.20, 0.34)

0.09 (−0.24, 0.41)

Aflib 2; PRN

−1.08 (−1.41, −0.76)

0.15 (−0.17, 0.48)

0.24 (−0.07, 0.55)

0.10 (−0.11, 0.30)

−0.75 (−1.08, −0.43)

0.22 (−0.03, 0.48)

0.23 (−0.08, 0.54)

0.14 (−0.09, 0.38)

Beva 1.25; PRN

−1.20 (−1.49, −0.93)

0.03 (−0.26, 0.33)

0.12 (−0.16, 0.39)

−0.03 (−0.28, 0.24)

−0.87 (−1.16, −0.59)

0.10 (−0.11, 0.30)

0.11 (−0.16, 0.38)

0.02 (−0.16, 0.20)

−0.12 (−0.27, 0.03)

Rani 0.5; PRN

−1.20 (−1.49, −0.89)

0.03 (−0.19, 0.26)

0.13 (−0.01, 0.27)

−0.02 (−0.28, 0.26)

−0.87 (−1.17, −0.57)

0.10 (−0.12, 0.33)

0.12 (−0.17, 0.40)

0.03 (−0.22, 0.29)

−0.12 (−0.46, 0.23)

0.01 (−0.30, 0.32)

Aflib 2; PRN+L

−1.05 (−1.33, −0.76)

0.18 (−0.10, 0.47)

0.27 (0.01, 0.54)

0.13 (−0.01, 0.27)

−0.72 (−1.00, −0.43)

0.25 (0.05, 0.46)

0.26 (−0.01, 0.53)

0.17 (−0.16, 0.52)

0.03 (−0.22, 0.29)

0.15 (−0.14, 0.45)

0.14 (−0.09, 0.38)

Beva 1.25; PRN+L

−1.17 (−1.41, −0.93)

0.05 (−0.18, 0.32)

0.15 (−0.07, 0.38)

0.00 (−0.20, 0.21)

−0.85 (−1.08, −0.60)

0.13 (−0.01, 0.27)

0.14 (−0.09, 0.36)

0.05 (−0.25, 0.36)

−0.10 (−0.38, 0.20)

0.03 (−0.22, 0.29)

0.02 (−0.16, 0.20)

−0.12 (−0.27, 0.03)

Rani 0.5; PRN+L

: Values given are z-scores (negative numbers favour the option on the right; positive numbers favour the option above)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

Figure 18BCVA: categorical change at 2 years (5-category; RE; meta-regression) – relative effect of all options versus sham

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 19BCVA: categorical change at 2 years (5-category; RE; meta-regression) – expected proportion of people in each category

Table 24BCVA: categorical change at 2 years (5-category; RE; meta-regression) – meta-regression coefficients

Covariate	Beta	(95%CrI)
PRN	0.10	(−0.11, 0.30)
Loading	0.03	(−0.22, 0.29)

: Values on probit scale (z-scores); positive values indicate worse BCVA

Table 25BCVA: categorical change at 2 years (5-category; RE; meta-regression) – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	13 (13, 13)
Aflib 0.5	0.051	5 (1, 11)
Aflib 2	0.326	2 (1, 7)
Beva 1.25	0.011	7 (2, 10)
PDT	0.000	12 (12, 12)
Rani 0.5	0.125	3 (1, 6)
Rani 2	0.339	3 (1, 9)
Aflib 2; PRN	0.080	6 (1, 11)
Beva 1.25; PRN	0.004	10 (3, 11)
Rani 0.5; PRN	0.042	6 (1, 10)
Aflib 2; PRN+Load	0.014	7 (2, 11)
Beva 1.25; PRN+Load	0.001	10 (6, 11)
Rani 0.5; PRN+Load	0.006	7 (3, 10)

Figure 20BCVA: categorical change at 2 years (5-category; RE; meta-regression) – rank probability histograms

Table 26BCVA: categorical change at 2 years (5-category; RE; meta-regression) – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	Between-study SD
102 (compared to 94 datapoints)	521.6	482.5	39.13	560.7	0.06 (95%CI: 0.00, 0.17)

G.2.1.3. Categorical (10-category)

G.2.1.3.1. Model selection

Model fit statistics for 12- and 24-month 10-category NMAs are shown in Table 27.

Table 27BCVA: categorical (10-category) at 12 and 24 months – summary model fit statistics, showing selection of best-fitting models

Outcome	Model for treatment differences	Number of discrete nodes	Model for category differences	Covariates					N	Total residual deviance	DIC	Standard deviation of random effects distributions (95%CrI)
Outcome	Model for treatment differences	Number of discrete nodes	Model for category differences	PRN	Loading	TREX	PRNX	Frequency	N	Total residual deviance	DIC	Between treatments	Between categories
Categorical change in BCVA at 12mo (10-category split)	FIXED	20	FIXED						221	484.0	1392	n/a	n/a
	FIXED		RANDOM							242.7	1188	n/a	0.14 (0.10, 0.19)
	RANDOM		FIXED							478.1	1392	0.08 (0.01, 0.18)	n/a
	RANDOM		RANDOM							237.5	1188	0.08 (0.01, 0.18)	0.14 (0.10, 0.19)
	RANDOM MR4c	7	FIXED	✓	✓	✓	✓	✓		479.3	1387	0.07 (0.01, 0.16)	n/a
	RANDOM MR4c	7	RANDOM	✓	✓	✓	✓	✓		241.6	1186	0.07 (0.01, 0.16)	0.13 (0.10, 0.18)
Categorical change in BCVA at 24mo (10-category split)	FIXED	12	FIXED						141	242.3	913.6	n/a	n/a
	FIXED		RANDOM							162.3	852.7	n/a	0.09 (0.06, 0.13)
	RANDOM		FIXED							240.8	915.1	0.06 (0.004, 0.20)	n/a
	RANDOM		RANDOM							161.2	854.0	0.05 (0.004, 0.18)	0.08 (0.06, 0.13)
	RANDOM MR2	7	FIXED	✓	✓	n/a	n/a	n/a		240.2	911.7	0.05 (0.004, 0.16)	n/a
	RANDOM MR2	7	RANDOM	✓	✓	n/a	n/a	n/a		160.8	851.4	0.04 (0.002, 0.14)	0.09 (0.06, 0.13)

: MR4a = 1 covariate shared between anti-VEGF agents for frequency–response effect; MR4b = separate covariates for each anti-VEGF agent for frequency–response effect; MR4c = 1 covariate for aflibercept and 1 covariate for bevacizumab and ranibizuamb for frequency–response effect;

G.2.1.3.2. Categorical change at 1 year (10-category; RE; meta-regression)

Table 28BCVA: categorical change at 1 year (10-category; RE; meta-regression) – input data

	Change in ETDRS letters		Aflib\|0.5\|1mo	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
	Minimum	Minimum	Aflib\|0.5\|1mo	Aflib\|2\|1mo	Aflib\|2\|Loading --> 2mo	Beva\|1.25\|1mo	Beva\|1.25\|2mo	Beva\|1.25\|6wk	Beva\|1.25\|Loading --> 12wk	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	Beva\|1.25\|Treat and extend	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> 3mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|Loading --> PRNX	Rani\|0.5\|PRN <6wkly	Rani\|0.5\|Treat and extend	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
ANCHOR 2006		−30											19	0
	−29	−15											32	14
	−14	−1											49	54
	0	+14											35	106
	+15	+29											8	80
	+30												0	26
Barikian 2015		−15								0	0
	−14	+14								18	20
	+15									12	10
BRAMD 2016		−15				18								8
	−14	+14				104								126
	+15					39								32
CATT 2011		−15				16					23			16				13
	−14	−5				18					23			19				23
	−4	+4				50					59			62				75
	+5	+14				98					90			90				103
	+15					83					76			97				71
El-Mollayess		+14				39					36
El-Mollayess	+15					21					24
EXCITE 2010		−30												0	4
	−29	−15												6	14
	−14	−1												14	55
	0	+14												62	127
	+15													33	38
GEFAL 2013		−15								17						18
	−14	−5								23						27
	−4	+4								47						47
	+5	+14								65						52
	+15									39						39
HARBOR		−15												6		15				18	14
	−14	+14												174		177				157	169
	+15													95		83				99	90
IVAN 2013		−30				2				1				3		0
	−29	−15				5				4				3		6
	−14	−5				22				15				13		14
	−4	+4				42				52				34		50
	+5	+14				44				39				51		44
	+15	+29				14				22				26		26
	+30					5				3				10		3
LUCAS 2015		−15										7							8
	−14	−5										9							2
	−4	+4										101							101
	+5	+14										20							26
	+15											47							50
Lushchyk 2013		−15				3	0	6
	−14	−5				4	6	4
	−4	+4				19	19	29
	+5	+14				14	22	10
	+15					6	7	8
MANTA 2013		−15								8						10
	−14	−5								24						25
	−4	+4								32						43
	+5	+14								54						50
	+15									36						35
MARINA		−15												26								90
	−14	+14												312								136
	+15													140								12
NATTB 2013		−15						3	5
	−14	+14						41	44
	+15							35	33
PIER		−15													16							32
	−14	+14													89							25
	+15														15							6
Sacu 2009		−15								0			2
	−14	−1								3			7
	0	+14								7			4
	+15									4			1
SALUTE 2015		−30														2	1
	−29	−15														2	3
	−14	−1														11	5
	0	+14														15	16
	+15															9	13
Subramanian 2010		−30								0						0
	−29	−15								0						1
	−14	−5								4						0
	−4	+4								2						2
	+5	+14								4						3
	+15	+29								3						0
	+30									2						1
TAP 1999		−30											59									49
	−29	−15											97									62
	−14	−5											93									47
	−4	+4											87									34
	+5	+14											42									10
	+15	+29											20									5
	+30												4									0
TREX 2015		−10												0					3
	−9	+9												11					24
	+10	+14												6					3
	+15													3					10
VIEW 1&2 POOLED		−15	29	32	31									34
	−14	+14	390	376	388									368
	+15		178	205	188									193
VIM 2005		−30											3									6
	−29	−15											7									12
	−14	−5											14									8
	−4	+4											5									9
	+5	+14											6									3
	+15												1									0
VIO		−30											39									20
	−29	−15											51									34
	−14	−5											56									30
	−4	+4											51									24
	+5												47									12
VIP 2001 Occ only		−30											37									30
	−29	−15											48									21
	−14	−5											25									19
	−4	+4											36									15
	+5	+14											15									5
	+15	+29											5									2
VIP 2001 PC or MC		−15											29									11
VIP 2001 PC or MC	−14												30									11

: Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

Table 29BCVA: categorical change at 1 year (10-category; RE; meta-regression) – relative effectiveness of all pairwise combinations

Sham

−1.3 (−1.6, −1.0)

Aflib 0.5

−1.4 (−1.8, −1.0)

−0.1 (−0.5, 0.3)

Aflib 2

−1.5 (−1.7, −1.2)

−0.2 (−0.4, 0.1)

−0.1 (−0.5, 0.3)

Beva 1.25

−0.2 (−0.4, −0.1)

1.1 (0.8, 1.4)

1.2 (0.7, 1.6)

1.2 (1.0, 1.5)

PDT

−1.5 (−1.7, −1.3)

−0.2 (−0.5, 0.0)

−0.1 (−0.5, 0.3)

0.0 (−0.1, 0.1)

−1.3 (−1.5, −1.0)

Rani 0.5

−1.3 (−1.6, −1.1)

0.0 (−0.3, 0.3)

0.1 (−0.4, 0.5)

0.1 (−0.1, 0.4)

−1.1 (−1.4, −0.8)

0.2 (0.0, 0.4)

Rani 2

−1.3 (−1.8, −0.9)

0.0 (−0.4, 0.4)

0.1 (−0.1, 0.2)

0.2 (−0.3, 0.6)

−1.1 (−1.5, −0.6)

0.2 (−0.2, 0.6)

0.0 (−0.4, 0.5)

Aflib 2 PRN

−1.4 (−1.7, −1.1)

−0.1 (−0.4, 0.2)

0.0 (−0.4, 0.5)

0.1 (−0.1, 0.2)

−1.1 (−1.4, −0.9)

0.1 (0.0, 0.3)

0.0 (−0.3, 0.2)

−0.1 (−0.5, 0.3)

Beva 1.25 PRN

−1.4 (−1.7, −1.1)

−0.1 (−0.4, 0.2)

0.0 (−0.4, 0.4)

0.1 (−0.1, 0.2)

−1.2 (−1.4, −0.9)

0.1 (−0.1, 0.2)

−0.1 (−0.3, 0.2)

−0.1 (−0.5, 0.3)

0.0 (−0.1, 0.1)

Rani 0.5 PRN

−1.3 (−1.8, −0.9)

0.0 (−0.4, 0.4)

0.1 (0.0, 0.2)

0.1 (−0.3, 0.6)

−1.1 (−1.5, −0.6)

0.2 (−0.2, 0.6)

0.0 (−0.4, 0.5)

0.0 (−0.2, 0.2)

0.0 (−0.4, 0.5)

0.1 (−0.3, 0.5)

Aflib 2 PRNL

−1.4 (−1.7, −1.1)

−0.1 (−0.4, 0.2)

0.0 (−0.4, 0.4)

0.1 (0.0, 0.2)

−1.2 (−1.4, −0.9)

0.1 (0.0, 0.3)

−0.1 (−0.3, 0.2)

−0.1 (−0.5, 0.4)

0.0 (−0.2, 0.2)

−0.1 (−0.5, 0.3)

Beva 1.25 PRNL

−1.4 (−1.7, −1.2)

−0.1 (−0.4, 0.1)

0.0 (−0.4, 0.4)

0.0 (−0.1, 0.2)

−1.2 (−1.5, −0.9)

0.1 (0.0, 0.2)

−0.1 (−0.3, 0.2)

−0.1 (−0.6, 0.3)

−0.1 (−0.3, 0.1)

0.0 (−0.2, 0.2)

−0.1 (−0.5, 0.3)

0.0 (−0.1, 0.1)

Rani 0.5 PRNL

−1.2 (−2.0, −0.5)

0.1 (−0.6, 0.8)

0.2 (−0.4, 0.8)

0.2 (−0.5, 1.0)

−1.0 (−1.7, −0.2)

0.3 (−0.4, 1.0)

0.1 (−0.6, 0.9)

0.1 (−0.6, 0.7)

0.1 (−0.6, 0.9)

0.2 (−0.6, 0.9)

0.1 (−0.5, 0.7)

0.2 (−0.6, 0.9)

0.2 (−0.5, 0.9)

Aflib 2 TREX

−1.3 (−2.0, −0.6)

0.0 (−0.7, 0.7)

0.1 (−0.6, 0.9)

0.2 (−0.4, 0.8)

−1.1 (−1.7, −0.4)

0.2 (−0.4, 0.9)

0.0 (−0.6, 0.7)

0.0 (−0.7, 0.8)

0.1 (−0.6, 0.7)

0.1 (−0.5, 0.8)

0.0 (−0.7, 0.8)

0.1 (−0.5, 0.7)

0.1 (−0.5, 0.8)

−0.1 (−0.5, 0.3)

Beva 1.25 TREX

−1.3 (−2.0, −0.7)

0.0 (−0.7, 0.6)

0.1 (−0.7, 0.8)

0.1 (−0.5, 0.8)

−1.1 (−1.7, −0.4)

0.2 (−0.4, 0.8)

0.0 (−0.6, 0.7)

0.0 (−0.8, 0.7)

0.0 (−0.6, 0.7)

0.1 (−0.6, 0.7)

0.0 (−0.7, 0.7)

0.1 (−0.6, 0.7)

0.1 (−0.5, 0.7)

−0.1 (−0.5, 0.3)

0.0 (−0.1, 0.1)

Rani 0.5 TREX

−1.7 (−2.3, −1.0)

−0.4 (−1.0, 0.3)

−0.2 (−0.8, 0.3)

−0.2 (−0.8, 0.5)

−1.4 (−2.1, −0.7)

−0.2 (−0.8, 0.5)

−0.3 (−1.0, 0.4)

−0.3 (−0.9, 0.2)

−0.3 (−0.9, 0.4)

−0.2 (−0.9, 0.4)

−0.3 (−0.8, 0.2)

−0.3 (−0.9, 0.4)

−0.2 (−0.9, 0.4)

−0.4 (−1.2, 0.4)

−0.4 (−1.3, 0.5)

−0.3 (−1.2, 0.6)

Aflib 2 PRNX

−1.7 (−2.3, −1.1)

−0.4 (−1.0, 0.2)

−0.3 (−1.0, 0.3)

−0.2 (−0.8, 0.3)

−1.5 (−2.0, −0.9)

−0.2 (−0.7, 0.3)

−0.4 (−0.9, 0.2)

−0.4 (−1.1, 0.3)

−0.3 (−0.9, 0.2)

−0.3 (−0.8, 0.2)

−0.4 (−1.0, 0.3)

−0.3 (−0.8, 0.2)

−0.5 (−1.4, 0.4)

−0.4 (−1.2, 0.4)

−0.1 (−0.5, 0.3)

Beva 1.25 PRNX

−1.8 (−2.3, −1.2)

−0.5 (−1.0, 0.1)

−0.3 (−1.0, 0.3)

−0.3 (−0.8, 0.3)

−1.5 (−2.1, −1.0)

−0.2 (−0.8, 0.3)

−0.4 (−1.0, 0.1)

−0.4 (−1.1, 0.2)

−0.4 (−0.9, 0.2)

−0.3 (−0.9, 0.2)

−0.4 (−1.1, 0.2)

−0.4 (−0.9, 0.2)

−0.3 (−0.8, 0.2)

−0.5 (−1.4, 0.3)

−0.5 (−1.3, 0.3)

−0.4 (−1.2, 0.4)

−0.1 (−0.5, 0.3)

0.0 (−0.1, 0.1)

Rani 0.5 PRNX

−1.4 (−1.6, −1.1)

−0.1 (−0.3, 0.2)

0.0 (−0.2, 0.3)

0.1 (−0.2, 0.4)

−1.1 (−1.4, −0.8)

0.1 (−0.1, 0.4)

0.0 (−0.3, 0.3)

−0.1 (−0.3, 0.2)

0.0 (−0.3, 0.3)

0.0 (−0.2, 0.3)

0.0 (−0.3, 0.2)

0.0 (−0.3, 0.3)

0.1 (−0.2, 0.3)

−0.1 (−0.8, 0.5)

−0.1 (−0.8, 0.6)

0.0 (−0.7, 0.6)

0.3 (−0.3, 0.8)

0.4 (−0.2, 0.9)

0.4 (−0.2, 1.0)

Aflib 2 2mo

−1.3 (−1.5, −1.1)

0.0 (−0.2, 0.2)

0.1 (−0.3, 0.5)

0.2 (0.1, 0.3)

−1.1 (−1.3, −0.9)

0.2 (0.1, 0.4)

0.0 (−0.2, 0.2)

0.0 (−0.4, 0.4)

0.1 (−0.1, 0.3)

0.0 (−0.4, 0.4)

0.1 (−0.1, 0.3)

−0.1 (−0.8, 0.6)

0.0 (−0.6, 0.6)

0.4 (−0.3, 1.0)

0.4 (−0.1, 0.9)

0.5 (−0.1, 1.0)

0.1 (−0.2, 0.3)

Beva 1.25 2mo

−1.3 (−1.5, −1.2)

0.0 (−0.3, 0.2)

0.1 (−0.3, 0.4)

0.1 (0.0, 0.3)

−1.1 (−1.3, −0.9)

0.2 (0.1, 0.3)

0.0 (−0.2, 0.2)

0.0 (−0.4, 0.4)

0.0 (−0.2, 0.2)

0.1 (−0.1, 0.3)

0.0 (−0.4, 0.4)

0.1 (−0.1, 0.3)

−0.1 (−0.8, 0.6)

0.0 (−0.7, 0.6)

0.0 (−0.6, 0.6)

0.3 (−0.3, 1.0)

0.4 (−0.2, 0.9)

0.4 (−0.1, 0.9)

0.0 (−0.2, 0.2)

0.0 (−0.1, 0.1)

Rani 0.5 2mo

−1.3 (−1.6, −1.0)

0.0 (−0.2, 0.2)

0.1 (−0.4, 0.5)

0.2 (−0.1, 0.4)

−1.1 (−1.4, −0.8)

0.2 (−0.1, 0.4)

0.0 (−0.3, 0.3)

0.0 (−0.5, 0.5)

0.1 (−0.2, 0.4)

0.0 (−0.5, 0.5)

0.1 (−0.2, 0.4)

−0.1 (−0.8, 0.6)

0.0 (−0.7, 0.6)

0.0 (−0.7, 0.7)

0.3 (−0.4, 1.0)

0.4 (−0.2, 1.0)

0.4 (−0.1, 1.0)

0.0 (−0.2, 0.3)

0.0 (−0.3, 0.2)

0.0 (−0.2, 0.2)

Aflib 2 3mo

−1.1 (−1.3, −0.9)

0.2 (−0.1, 0.4)

0.3 (−0.1, 0.7)

0.3 (0.1, 0.6)

−0.9 (−1.1, −0.7)

0.4 (0.2, 0.6)

0.2 (0.0, 0.4)

0.2 (−0.3, 0.6)

0.2 (0.0, 0.5)

0.3 (0.0, 0.6)

0.2 (−0.2, 0.6)

0.3 (0.0, 0.5)

0.3 (0.0, 0.6)

0.1 (−0.6, 0.8)

0.2 (−0.5, 0.8)

0.5 (−0.1, 1.2)

0.6 (0.0, 1.1)

0.6 (0.0, 1.2)

0.2 (0.0, 0.5)

0.2 (0.1, 0.3)

0.2 (0.1, 0.4)

0.2 (−0.1, 0.5)

Beva 1.25 3mo

−1.2 (−1.3, −1.0)

0.1 (−0.1, 0.4)

0.2 (−0.2, 0.6)

0.3 (0.1, 0.5)

−0.9 (−1.1, −0.7)

0.3 (0.1, 0.6)

0.2 (0.0, 0.4)

0.1 (−0.3, 0.6)

0.2 (−0.1, 0.5)

0.2 (0.0, 0.5)

0.2 (−0.3, 0.6)

0.2 (0.0, 0.5)

0.3 (0.0, 0.5)

0.1 (−0.7, 0.8)

0.1 (−0.5, 0.8)

0.2 (−0.5, 0.8)

0.5 (−0.2, 1.1)

0.6 (0.0, 1.1)

0.6 (0.0, 1.1)

0.2 (0.0, 0.4)

0.1 (0.0, 0.3)

0.2 (0.1, 0.3)

0.2 (−0.1, 0.4)

0.0 (−0.1, 0.1)

Rani 0.5 3mo

: Values given are z-scores (option on the right versus option above, with negative numbers favouring the option on the right)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

Figure 21BCVA: categorical change at 1 year (10-category; RE; meta-regression) – relative effect of all options versus sham

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 22BCVA: categorical change at 1 year (10-category; RE; meta-regression) – expected proportion of people in each category

Table 30BCVA: categorical change at 1 year (10-category; RE; meta-regression) – meta-regression coefficients

Covariate		Beta	(95%CrI)
PRN		0.10	(−0.05, 0.24)
Loading		−0.02	(−0.20, 0.17)
TREX		0.18	(−0.43, 0.81)
PRNX		−0.33	(−0.83, 0.18)
Frequency (per additional month)	Aflibercept	0.04	(−0.18, 0.26)
Frequency (per additional month)	Bevacizumab / ranibizumab	0.17	(0.07, 0.28)

: Values on probit scale (z-scores); positive values indicate worse BCVA

Table 31BCVA: categorical change at 1 year (10-category; RE; meta-regression) – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	25 (25, 25)
Aflib 0.5	0.002	16 (5, 22)
Aflib 2	0.031	9 (1, 20)
Beva 1.25	0.019	7 (2, 14)
PDT	0.000	24 (24, 24)
Rani 0.5	0.056	5 (1, 11)
Rani 2	0.006	14 (4, 21)
Aflib 2; PRN	0.004	16 (3, 23)
Beva 1.25; PRN	0.001	12 (4, 21)
Rani 0.5; PRN	0.006	10 (3, 19)
Aflib 2; PRN+Load	0.002	15 (3, 23)
Beva 1.25; PRN+Load	0.001	11 (4, 20)
Rani 0.5; PRN+Load	0.004	9 (3, 18)
Aflib 2; TREX	0.031	19 (1, 23)
Beva 1.25; TREX	0.020	16 (2, 23)
Rani 0.5; TREX	0.059	14 (1, 22)
Aflib 2; PRNX	0.209	3 (1, 22)
Beva 1.25; PRNX	0.127	3 (1, 20)
Rani 0.5; PRNX	0.413	2 (1, 18)
Aflib 2; 2mo	0.000	12 (5, 18)
Beva 1.25; 2mo	0.000	16 (9, 21)
Rani 0.5; 2mo	0.000	14 (7, 19)
Aflib 2; 3mo	0.007	15 (4, 22)
Beva 1.25; 3mo	0.000	22 (15, 23)
Rani 0.5; 3mo	0.000	21 (14, 23)

Figure 23BCVA: categorical change at 1 year (10-category; RE; meta-regression) – rank probability histograms

Table 32BCVA: categorical change at 1 year (10-category; RE; meta-regression) – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	Between-study SD
241.6 (compared to 221 datapoints)	1099	1011	87.33	1186	0.07 (95%CI: 0.01, 0.16)

G.2.1.3.3. Categorical change at 2 years (10-category; RE; meta-regression)

Table 33BCVA: categorical change at 2 years (10-category; RE; meta-regression) – input data

	Change in ETDRS letters		Aflib\|0.5\|Loading-->PRN	Aflib\|2\| Loading-->PRN	Beva\|1.25\|1mo	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|PRN <6wkly	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
	Minimum	Minimum	Aflib\|0.5\|Loading-->PRN	Aflib\|2\| Loading-->PRN	Beva\|1.25\|1mo	Beva\|1.25\|Loading --> PRN <6wkly	Beva\|1.25\|PRN <6wkly	PDT\|\|PRN >6wkly	Rani\|0.5\|1mo	Rani\|0.5\|Loading --> PRN <6wkly	Rani\|0.5\|PRN <6wkly	Rani\|2\|1mo	Rani\|2\|Loading --> PRN <6wkly	Sham\|\|
ANCHOR 2006		−30						23	2
	−29	−15						26	29
	−14	−1						53	32
	0	+14						32	112
	+15	+29						6	73
	+30							3	32
CATT 2011		−15			10		29		9		19
	−14	+14			78		151		81		164
	+15				41		71		44		81
HARBOR		−15							16	25		27	23
	−14	+14							164	159		144	155
	+15								95	91		103	95
IVAN 2013		−30			4	0			4	4
	−29	−15			8	11			4	11
	−14	−5			19	11			12	19
	−4	+4			35	36			33	32
	+5	+14			36	48			39	47
	+15	+29			19	15			32	18
	+30				5	2			9	4
MARINA		−15							43					112
	−14	+14							293					117
	+15								142					9
TAP 1999		−30						73						62
	−29	−15						116						67
	−14	−5						92						31
	−4	+4						59						26
	+5	+14						26						13
	+15	+29						33						8
	+30							3						0
VIEW 1&2 POOLED		−30	▬^a	▬^b						▬^b
	−29	−15	▬^b	▬^b						▬^b
	−14	−10	▬^b	▬^b						▬^b
	−9	−5	▬^b	▬^b						▬^b
	−4	−1	▬^b	▬^b						▬^b
	0	+4	▬^b	▬^b						▬^b
	+5	+9	▬^b	▬^b						▬^b
	+10	+14	▬^b	▬^b						▬^b
	+15	+29	▬^b	▬^b						▬^b
	+30		▬^b	▬^b						▬^b
VIM 2005		−30						4						13
	−29	−15						13						10
	−14	−5						4						5
	−4	+4						4						5
	+5	+14						4						3
	+15							3						1
VIO		−30						56						30
	−29	−15						59						34
	−14	−5						43						30
	−4	+4						48						19
	+5							38						7
VIP 2001 Occ only		−30						48						43
	−29	−15						43						20
	−14	−5						29						10
	−4	+4						25						14
	+5	+14						13						4
	+15	+29						8						1
VIP 2001 PC or MC		−30						19						11
	−29	−15						11						2
	−14							29						9

: Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

Table 34BCVA: categorical change at 2 years (10-category; RE; meta-regression) – relative effectiveness of all pairwise combinations

Sham

−1.26 (−1.51, −1.02)

Aflib 0.5

−1.35 (−1.58, −1.12)

−0.09 (−0.23, 0.06)

Aflib 2

−1.24 (−1.46, −1.02)

0.03 (−0.19, 0.25)

0.11 (−0.09, 0.31)

Beva 1.25

−0.31 (−0.43, −0.18)

0.95 (0.70, 1.19)

1.04 (0.80, 1.27)

0.93 (0.70, 1.15)

PDT

−1.35 (−1.52, −1.17)

−0.09 (−0.26, 0.08)

0.00 (−0.15, 0.15)

−0.11 (−0.25, 0.02)

−1.04 (−1.21, −0.86)

Rani 0.5

−1.36 (−1.61, −1.12)

−0.10 (−0.33, 0.14)

−0.01 (−0.24, 0.21)

−0.12 (−0.34, 0.09)

−1.05 (−1.29, −0.81)

−0.01 (−0.18, 0.15)

Rani 2

−1.25 (−1.55, −0.94)

0.01 (−0.24, 0.26)

0.10 (−0.10, 0.29)

−0.02 (−0.30, 0.27)

−0.94 (−1.24, −0.63)

0.09 (−0.15, 0.34)

0.11 (−0.19, 0.40)

Aflib 2 PRN

−1.14 (−1.43, −0.85)

0.12 (−0.17, 0.41)

0.21 (−0.07, 0.48)

0.10 (−0.10, 0.29)

−0.83 (−1.12, −0.53)

0.21 (−0.03, 0.45)

0.22 (−0.07, 0.51)

0.11 (−0.09, 0.31)

Beva 1.25 PRN

−1.25 (−1.51, −0.99)

0.01 (−0.25, 0.27)

0.10 (−0.14, 0.33)

−0.02 (−0.26, 0.22)

−0.94 (−1.20, −0.68)

0.10 (−0.10, 0.29)

0.11 (−0.15, 0.36)

0.00 (−0.15, 0.15)

−0.11 (−0.25, 0.02)

Rani 0.5 PRN

−1.25 (−1.51, −0.99)

0.01 (−0.18, 0.20)

0.10 (−0.03, 0.22)

−0.01 (−0.25, 0.22)

−0.94 (−1.20, −0.68)

0.09 (−0.09, 0.29)

0.11 (−0.14, 0.37)

0.00 (−0.23, 0.23)

−0.11 (−0.41, 0.19)

0.00 (−0.27, 0.27)

Aflib 2 PRN+Load

−1.14 (−1.40, −0.88)

0.12 (−0.13, 0.37)

0.21 (−0.03, 0.44)

0.10 (−0.03, 0.22)

−0.83 (−1.09, −0.57)

0.21 (0.02, 0.39)

0.22 (−0.03, 0.47)

0.11 (−0.20, 0.42)

0.00 (−0.23, 0.23)

0.11 (−0.16, 0.38)

0.11 (−0.09, 0.31)

Beva 1.25 PRN+Load

−1.25 (−1.47, −1.03)

0.01 (−0.20, 0.22)

0.10 (−0.10, 0.29)

−0.02 (−0.20, 0.17)

−0.94 (−1.16, −0.72)

0.10 (−0.03, 0.22)

0.11 (−0.10, 0.31)

0.00 (−0.28, 0.28)

−0.11 (−0.38, 0.15)

0.00 (−0.23, 0.23)

0.00 (−0.15, 0.15)

−0.11 (−0.25, 0.02)

Rani 0.5 PRN+Load

: Values given are z-scores (negative numbers favour the option on the right; positive numbers favour the option above)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

Figure 24BCVA: categorical change at 2 years (10-category; RE; meta-regression) – relative effect of all options versus common comparator

Values less than 0 favour sham; values greater than 0 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 25BCVA: categorical change at 2 years (10-category; RE; meta-regression) – expected proportion of people in each category

Table 35BCVA: categorical change at 2 years (5-category; RE; meta-regression) – meta-regression coefficients

Covariate	Beta	(95%CrI)
PRN	0.10	(−0.10, 0.29)
Loading	0.00	(−0.23, 0.23)

: Values on probit scale (z-scores); positive values indicate worse BCVA

Table 36BCVA: categorical change at 2 years (10-category; RE; meta-regression) – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	13 (13, 13)
Aflib 0.5	0.030	6 (1, 11)
Aflib 2	0.257	3 (1, 8)
Beva 1.25	0.014	7 (2, 10)
PDT	0.000	12 (12, 12)
Rani 0.5	0.161	3 (1, 6)
Rani 2	0.395	2 (1, 9)
Aflib 2; PRN	0.062	6 (1, 11)
Beva 1.25; PRN	0.004	10 (3, 11)
Rani 0.5; PRN	0.046	6 (1, 10)
Aflib 2; PRN+Load	0.017	6 (2, 11)
Beva 1.25; PRN+Load	0.002	10 (5, 11)
Rani 0.5; PRN+Load	0.013	6 (2, 10)

Figure 26BCVA: categorical change at 2 years (10-category; RE; meta-regression) – rank probability histograms

Table 37BCVA: categorical change at 2 years (10-category; RE; meta-regression) – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	tau
160.8 (compared to 141 datapoints)	802.4	753.8	48.61	851	0.04 (95%CI: 0.00, 0.14)

G.2.2. Discontinuation

G.2.2.1. Model selection

Model fit statistics for the discontinuation NMA are shown in Table 16.

As noted in G.1.1.4, once we had selected the optimal model for the most critical NMA (bivariate normal mean difference at 12 and 24 months; see G.2.1.1.1.1), model selection for other outcomes sought to disprove that this was the globally optimal model, rather than to establish what could be argued to be best for that particular outcome. In this instance, it was clear that the preferred (random-effects, MR4c) approach was no worse than fixed and/or unadjusted models, so we were happy to use the same approach for this outcome.

Table 38BCVA: categorical (5-category) at 12 and 24 months – summary model fit statistics, showing selection of best-fitting models

Outcome	Model for treatment differences	Number of discrete nodes	Covariates					N	Total residual deviance	DIC	Standard deviation of random effects distribution (95%CrI)
Outcome	Model for treatment differences	Number of discrete nodes	PRN	Loading	TREX	PRNX	Frequency	N	Total residual deviance	DIC	Standard deviation of random effects distribution (95%CrI)
Probability of discontinuation at 12mo	FIXED	20						59	65.34	355.9	n/a
	FIXED MR4c	7	✓	✓	✓	✓	✓		72.75	356.5	n/a
	RANDOM	20							61.88	357.2	0.22 (0.01, 0.67)
	RANDOM MR4c	7	✓	✓	✓	✓	✓		62.82	355.1	0.29 (0.03, 0.62)

: MR4c = 1 covariate for aflibercept and 1 covariate for bevacizumab and ranibizuamb for frequency–response effect

G.2.2.2. Probability of discontinuation at 1 year (RE; meta-regression)

Figure 27Probability of discontinuation at 1 year (RE; meta-regression) – evidence network

Table 39Probability of discontinuation at 1 year (RE; meta-regression) – input data

	Rani 0.5 1mo	Rani 0.5 Loading --> 3mo	Rani 0.5 Loading --> PRN <6wkly	Rani 0.5 Loading --> PRNX	Rani 0.5 PRN <6wkly	Rani 0.5 Treat and extend	Rani 2 1mo	Rani 2 Loading --> PRN <6wkly	Aflib 0.5 1mo	Aflib 2 1mo	Aflib 2 Loading --> 2mo	Beva 1.25 1mo	Beva 1.25 2mo	Beva 1.25 6wk	Beva 1.25 Loading --> 12wk	Beva 1.25 Loading --> PRN <6wkly	Beva 1.25 PRN <6wkly	Beva 1.25 Treat and extend	PDT PRN >6wkly	Sham
ANCHOR 2006	14/280																		13/140
BISWAS 2011			8/62													10/60
BRAMD 2016	29/166											34/166
CATT 2011	17/301				13/298							21/286					29/300
EXCITE 2010	12/115	37/238
GEFAL 2013			56/239													55/246
HARBOR	21/275		16/275				18/274	18/273
IVAN 2013	17/157		12/155									15/149				9/145
LUCAS 2015						34/221												36/220
Lushchyk 2013												18/64	10/64	6/63
MANTA 2013			36/163													33/154
MARINA	16/478																			26/238
NATTB 2013														12/94	12/91
PIER		4/121																		9/63
Sacu 2009																0/14			1/14
SALUTE 2015			6/45	10/48
Subramanian 2010			1/8													5/20
TAP 1999																			23/402	13/207
TREX 2015	1/20					6/40
VIEW 1&2 POOLED	71/609								82/615	58/617	81/616
VIM 2005																			3/39	2/40
VIO																			25/244	9/120
VIP 2001 ALL																			15/225	10/114

: Where individual trials have more than 1 arm representing a treatment option, they have been pooled in this table for ease of interpretation, although they are entered as separate datapoints in the NMA.

Table 40Probability of discontinuation at 1 year (RE; meta-regression) – relative effectiveness of all pairwise combinations

Sham
0.37 (0.13, 0.98)	Aflib 0.5
0.17 (0.04, 0.74)	0.47 (0.12, 1.77)	Aflib 2
0.36 (0.16, 0.81)	0.96 (0.40, 2.40)	2.08 (0.51, 9.02)	Beva 1.25
0.92 (0.56, 1.53)	2.48 (0.93, 7.17)	5.31 (1.24, 25.52)	2.58 (1.11, 6.00)	PDT
0.31 (0.14, 0.66)	0.84 (0.37, 1.96)	1.81 (0.46, 7.47)	0.87 (0.63, 1.18)	0.34 (0.15, 0.73)	Rani 0.5
0.31 (0.12, 0.77)	0.84 (0.30, 2.34)	1.80 (0.40, 8.45)	0.87 (0.38, 1.93)	0.34 (0.13, 0.86)	1.00 (0.47, 2.10)	Rani 2
0.19 (0.04, 0.86)	0.50 (0.11, 2.09)	1.07 (0.62, 1.84)	0.52 (0.10, 2.36)	0.20 (0.04, 0.94)	0.60 (0.13, 2.57)	0.60 (0.11, 2.87)	Aflib 2 PRN
0.38 (0.15, 0.98)	1.03 (0.38, 2.84)	2.22 (0.51, 10.20)	1.07 (0.62, 1.84)	0.41 (0.16, 1.07)	1.23 (0.70, 2.17)	1.23 (0.48, 3.16)	2.08 (0.51, 9.02)	Beva 1.25 PRN
0.33 (0.13, 0.84)	0.90 (0.33, 2.43)	1.94 (0.44, 8.72)	0.94 (0.46, 1.83)	0.36 (0.14, 0.92)	1.07 (0.62, 1.84)	1.07 (0.42, 2.71)	1.81 (0.46, 7.47)	0.87 (0.63, 1.18)	Rani 0.5 PRN
0.12 (0.02, 0.55)	0.34 (0.08, 1.35)	0.72 (0.44, 1.14)	0.35 (0.07, 1.50)	0.14 (0.03, 0.60)	0.40 (0.09, 1.67)	0.40 (0.08, 1.87)	0.67 (0.33, 1.36)	0.32 (0.07, 1.50)	0.37 (0.08, 1.73)	Aflib 2 PRNL
0.26 (0.10, 0.64)	0.69 (0.25, 1.89)	1.49 (0.33, 6.84)	0.72 (0.44, 1.14)	0.28 (0.11, 0.71)	0.82 (0.46, 1.43)	0.82 (0.32, 2.13)	1.39 (0.28, 7.33)	0.67 (0.33, 1.36)	0.76 (0.34, 1.77)	2.08 (0.51, 9.02)	Beva 1.25 PRNL
0.22 (0.09, 0.53)	0.60 (0.23, 1.59)	1.31 (0.30, 5.77)	0.63 (0.34, 1.10)	0.24 (0.10, 0.59)	0.72 (0.44, 1.14)	0.72 (0.29, 1.76)	1.22 (0.25, 6.03)	0.59 (0.27, 1.21)	0.67 (0.33, 1.36)	1.81 (0.46, 7.47)	0.87 (0.63, 1.18)	Rani 0.5 PRNL
0.82 (0.06, 32.11)	2.21 (0.17, 78.63)	4.65 (0.55, 143.4)	2.28 (0.17, 87.09)	0.89 (0.06, 34.75)	2.63 (0.20, 97.36)	2.64 (0.18, 106.6)	4.37 (0.47, 143.1)	2.14 (0.15, 83.20)	2.45 (0.17, 95.81)	6.50 (0.72, 208.5)	3.24 (0.23, 122.6)	3.68 (0.27, 141.3)	Aflib 2 TREX
1.68 (0.17, 56.72)	4.54 (0.44, 157.1)	10.00 (0.74, 416.8)	4.65 (0.55, 143.4)	1.83 (0.18, 60.64)	5.34 (0.61, 165.8)	5.40 (0.53, 183.8)	9.32 (0.65, 405.5)	4.37 (0.47, 143.1)	5.04 (0.53, 165.8)	13.98 (1.00, 590.1)	6.50 (0.72, 208.5)	7.50 (0.81, 242.4)	2.08 (0.51, 9.02)	Beva 1.25 TREX
1.46 (0.15, 49.34)	3.95 (0.39, 134.7)	8.71 (0.65, 349.1)	4.05 (0.46, 126.6)	1.59 (0.16, 52.88)	4.65 (0.55, 143.4)	4.70 (0.47, 158.9)	8.20 (0.58, 345.8)	3.79 (0.41, 122.2)	4.37 (0.47, 143.1)	12.27 (0.88, 502.1)	5.67 (0.62, 185.2)	6.50 (0.72, 208.5)	1.81 (0.46, 7.47)	0.87 (0.63, 1.18)	Rani 0.5 TREX
0.22 (0.03, 1.63)	0.58 (0.08, 4.09)	1.26 (0.31, 5.26)	0.61 (0.08, 4.44)	0.24 (0.03, 1.75)	0.70 (0.09, 5.04)	0.69 (0.09, 5.37)	1.18 (0.27, 5.36)	0.56 (0.07, 4.28)	0.65 (0.08, 5.01)	1.75 (0.48, 6.85)	0.85 (0.12, 5.89)	0.97 (0.14, 6.72)	0.26 (0.01, 3.73)	0.12 (0.00, 2.49)	0.14 (0.00, 2.84)	Aflib 2 PRNX
0.45 (0.09, 2.28)	1.21 (0.23, 6.53)	2.63 (0.37, 19.41)	1.26 (0.31, 5.26)	0.49 (0.10, 2.51)	1.44 (0.36, 6.25)	1.44 (0.29, 7.43)	2.44 (0.32, 19.70)	1.18 (0.27, 5.36)	1.35 (0.29, 6.54)	3.66 (0.56, 25.91)	1.75 (0.48, 6.85)	2.00 (0.54, 8.20)	0.54 (0.01, 10.93)	0.26 (0.01, 3.73)	0.30 (0.01, 4.37)	2.08 (0.51, 9.02)	Beva 1.25 PRNX
0.39 (0.08, 1.92)	1.06 (0.21, 5.55)	2.29 (0.33, 16.25)	1.10 (0.26, 4.70)	0.43 (0.09, 2.10)	1.26 (0.31, 5.26)	1.27 (0.26, 6.33)	2.14 (0.28, 16.78)	1.03 (0.23, 4.68)	1.18 (0.27, 5.36)	3.20 (0.50, 21.60)	1.53 (0.40, 6.11)	1.75 (0.48, 6.85)	0.47 (0.01, 9.19)	0.23 (0.01, 3.22)	0.26 (0.01, 3.73)	1.81 (0.46, 7.47)	0.87 (0.63, 1.18)	Rani 0.5 PRNX
0.25 (0.09, 0.66)	0.67 (0.31, 1.46)	1.45 (0.67, 3.23)	0.70 (0.28, 1.70)	0.27 (0.09, 0.73)	0.80 (0.34, 1.85)	0.80 (0.29, 2.24)	1.35 (0.53, 3.65)	0.65 (0.24, 1.80)	0.75 (0.27, 2.05)	2.02 (0.84, 5.17)	0.97 (0.35, 2.70)	1.11 (0.42, 3.00)	0.31 (0.01, 3.06)	0.15 (0.00, 1.54)	0.17 (0.00, 1.74)	1.16 (0.23, 5.75)	0.55 (0.10, 2.87)	0.64 (0.12, 3.19)	Aflib 2 2mo
0.36 (0.18, 0.72)	0.98 (0.43, 2.29)	2.10 (0.53, 8.86)	1.02 (0.73, 1.40)	0.39 (0.19, 0.81)	1.17 (0.74, 1.81)	1.17 (0.56, 2.48)	1.96 (0.45, 9.69)	0.95 (0.50, 1.78)	1.09 (0.51, 2.33)	2.93 (0.71, 13.47)	1.41 (0.79, 2.57)	1.62 (0.84, 3.23)	0.45 (0.01, 5.77)	0.22 (0.01, 1.89)	0.25 (0.01, 2.22)	1.68 (0.24, 12.43)	0.81 (0.19, 3.34)	0.92 (0.21, 4.02)	1.45 (0.63, 3.39)	Beva 1.25 2mo
0.32 (0.17, 0.58)	0.85 (0.40, 1.85)	1.84 (0.48, 7.34)	0.89 (0.56, 1.38)	0.34 (0.17, 0.66)	1.02 (0.73, 1.40)	1.02 (0.51, 2.01)	1.71 (0.41, 7.78)	0.83 (0.43, 1.57)	0.95 (0.50, 1.78)	2.56 (0.63, 11.16)	1.23 (0.64, 2.43)	1.41 (0.79, 2.57)	0.39 (0.01, 4.91)	0.19 (0.01, 1.70)	0.22 (0.01, 1.89)	1.46 (0.21, 10.48)	0.71 (0.16, 2.98)	0.81 (0.19, 3.34)	1.27 (0.58, 2.78)	0.87 (0.63, 1.18)	Rani 0.5 2mo
0.36 (0.13, 0.95)	0.98 (0.46, 2.15)	2.11 (0.45, 10.40)	1.02 (0.41, 2.45)	0.39 (0.14, 1.06)	1.17 (0.50, 2.68)	1.17 (0.43, 3.28)	1.95 (0.39, 10.92)	0.95 (0.34, 2.58)	1.09 (0.40, 2.95)	2.92 (0.61, 15.80)	1.42 (0.52, 3.90)	1.62 (0.62, 4.34)	0.44 (0.01, 6.55)	0.22 (0.01, 2.26)	0.25 (0.01, 2.53)	1.67 (0.21, 13.92)	0.81 (0.15, 4.11)	0.92 (0.18, 4.68)	1.45 (0.67, 3.23)	1.00 (0.43, 2.28)	1.14 (0.53, 2.50)	Aflib 2 3mo
0.37 (0.18, 0.73)	1.00 (0.41, 2.44)	2.14 (0.52, 9.20)	1.03 (0.54, 1.95)	0.40 (0.18, 0.83)	1.18 (0.58, 2.40)	1.18 (0.52, 2.68)	2.00 (0.43, 9.85)	0.97 (0.41, 2.21)	1.11 (0.43, 2.82)	2.98 (0.69, 14.09)	1.44 (0.63, 3.28)	1.65 (0.69, 3.99)	0.45 (0.01, 6.00)	0.22 (0.01, 2.09)	0.25 (0.01, 2.48)	1.71 (0.23, 12.80)	0.82 (0.17, 3.80)	0.94 (0.19, 4.53)	1.48 (0.60, 3.60)	1.02 (0.73, 1.40)	1.17 (0.74, 1.81)	1.02 (0.42, 2.47)	Beva 1.25 3mo
0.32 (0.17, 0.60)	0.87 (0.38, 1.97)	1.88 (0.47, 7.67)	0.90 (0.43, 1.82)	0.35 (0.17, 0.68)	1.03 (0.54, 1.95)	1.04 (0.48, 2.17)	1.75 (0.39, 8.06)	0.84 (0.35, 1.94)	0.97 (0.41, 2.21)	2.61 (0.61, 11.75)	1.26 (0.53, 3.03)	1.44 (0.63, 3.28)	0.40 (0.01, 5.03)	0.19 (0.01, 1.86)	0.22 (0.01, 2.09)	1.49 (0.20, 10.86)	0.72 (0.14, 3.39)	0.82 (0.17, 3.80)	1.30 (0.55, 2.95)	0.89 (0.56, 1.38)	1.02 (0.73, 1.40)	0.89 (0.38, 2.00)	0.87 (0.63, 1.18)	Rani 0.5 3mo

: Values given are odds ratios (values less than 1 favour the option on the right; values greater than 1 favour the option above)
: Data are derived from the network meta-analysis, reflecting direct and indirect evidence of treatment effects. The point estimate reflects the mean of the posterior distribution, and numbers in parentheses are 95% credible intervals.

Figure 28Probability of discontinuation at 1 year (RE; meta-regression) – relative effect of all options versus sham

Values greater than 1 favour sham; values less than 1 favour the comparator treatment. Error bars are 95% credible intervals.

Figure 29Probability of discontinuation at 1 year (RE; meta-regression) – absolute discontinuation rates

Table 41Probability of discontinuation at 1 year (RE; meta-regression) – meta-regression coefficients

Covariate		Beta	(95%CrI)
PRN		0.07	(−0.48, 0.61)
Loading		−0.40	(−1.12, 0.31)
TREX		1.70	(−0.60, 4.97)
PRNX		0.57	(−0.74, 1.92)
Frequency (per additional month)	Aflibercept	0.38	(−0.40, 1.17)
Frequency (per additional month)	Bevacizumab / ranibizumab	0.02	(−0.31, 0.33)

: Values on ln(odds) scale; positive values indicate higher probability of dropout

Table 42Probability of discontinuation at 1 year (RE; meta-regression) – rankings for each comparator

	Probability best	Median rank (95%CI)
Sham	0.000	22 (18, 25)
Aflib 0.5	0.006	15 (4, 23)
Aflib 2	0.024	4 (2, 19)
Beva 1.25	0.001	14 (5, 21)
PDT	0.000	22 (17, 25)
Rani 0.5	0.001	11 (4, 18)
Rani 2	0.031	11 (1, 21)
Aflib 2; PRN	0.073	4 (1, 21)
Beva 1.25; PRN	0.002	16 (5, 22)
Rani 0.5; PRN	0.010	13 (3, 21)
Aflib 2; PRN+Load	0.518	1 (1, 16)
Beva 1.25; PRN+Load	0.021	8 (2, 18)
Rani 0.5; PRN+Load	0.065	6 (1, 15)
Aflib 2; TREX	0.035	21 (1, 25)
Beva 1.25; TREX	0.001	24 (6, 25)
Rani 0.5; TREX	0.005	24 (4, 25)
Aflib 2; PRNX	0.148	5 (1, 23)
Beva 1.25; PRNX	0.006	18 (3, 25)
Rani 0.5; PRNX	0.023	16 (2, 24)
Aflib 2; 2mo	0.000	7 (4, 18)
Beva 1.25; 2mo	0.000	15 (7, 20)
Rani 0.5; 2mo	0.000	11 (5, 17)
Aflib 2; 3mo	0.018	15 (2, 23)
Beva 1.25; 3mo	0.004	15 (4, 22)
Rani 0.5; 3mo	0.009	12 (3, 20)

Figure 30Probability of discontinuation at 1 year (RE; meta-regression) – rank probability histograms

Table 43Probability of discontinuation at 1 year (RE; meta-regression) – model fit statistics

Residual deviance	Dbar	Dhat	pD	DIC	sd
62.82 (compared to 59 datapoints)	311.6	268.1	43.51	355.1	0.29 (95%CI: 0.03, 0.62)

G.3. References

Achana FA, Cooper NJ, Bujkiewicz S, Hubbard SJ, Kendrick D, Jones DR and Sutton AJ. Network meta-analysis of multiple outcome measures accounting for borrowing of information across outcomes. BMC Medical Research Methodology 2014;14:92. [PMC free article: PMC4142066] [PubMed: 25047164]
Bujkiewicz S, Thompson JR, Riley RD, Abrams KR. Bayesian meta-analytical methods to incorporate multiple surrogate endpoints in drug development process. Statistics in Medicine, 2016; 35 (7): 1063–89. [PMC free article: PMC4950070] [PubMed: 26530518]
Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. NICE DSU Technical Support Document 2: A generalised linear modelling framework for pairwise and network meta-analysis of randomised controlled trials. 2011; last updated September 2016; available from http://www.nicedsu.org.uk [PubMed: 27466657]
Dias, S., Sutton, A.J., Welton, N.J., Ades, A.E. NICE DSU Technical Support Document 3: Heterogeneity: subgroups, meta-regression, bias and bias-adjustment. 2011; last updated April 2012; available from http://www.nicedsu.org.uk [PubMed: 27905717]
Dias, S., Welton, N.J., Sutton, A.J., Ades, A.E. NICE DSU Technical Support Document 5: Evidence synthesis in the baseline natural history model. 2011; last updated April 2012; available from http://www.nicedsu.org.uk [PubMed: 27466660]
Franchini AJ, Dias S, Ades AE, Jansen JP, Welton NJ. Accounting for correlation in network meta-analysis with multi-arm trials. Research synthesis methods. 2012 Jun 1;3(2):142–60. [PubMed: 26062087]
Lu G, Ades AE, Sutton AJ, Cooper NJ, Briggs AH, Caldwell DM. Meta-analysis of mixed treatment comparisons at multiple follow-up times. Statistics in medicine. 2007 Sep 10;26(20):3681–99. [PubMed: 17285571]
Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology). 2002 Oct 1;64(4):583–639.

G.4. OpenBUGS code

Code is provided below for the NMA and baseline synthesis models that were selected for use in the guideline +/− health economic model. In several respects, this code is written in such a way as to facilitiate different models being run by changing input data rather than by altering model code itself. Other models described in the ‘model selection’ tables above used identical or similar code, but have not been reproduced here, for clarity’s sake.

G.4.1. Network meta-analyses

G.4.1.1. Continuous data

Bivariate normal model for 1- and 2-year data, with provision for SMD and meta-regression (random effects)

# Bivariate normal likelihood; identity link 
# Random-effects model for multi-arm trials 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Sutton, A.J., Welton, N.J. & Ades, A.E. 
# NICE DSU Technical Support Document 3: Heterogeneity: subgroups, meta-regression, 
# bias and bias-adjustment. 2011; last updated April 2012. 
# http://www.nicedsu.org.uk 
# 
# This model will generate results on a natural scale if blnSMD is set to 0, 
# and an SMD scale if blnSMD is set to 1 
# It will include covariates if numCovars is set to > 1 and blnCovars!= c(0,0,0,0) 
# blnCovars[1] is a switch for PRN 
# blnCovars[2] is a switch for Load 
# blnCovars[3] is a switch for TREX and PRNX 
# blnCovars[4] is a switch for Frequency 
# Outputs are calculated with and without covariates for treatments identifed in core c()
model { 
for(i in 1:NumStudies.0_12only) { # indexes studies 
mu[i,1] ~ dnorm(0, .0001) # vague priors for trial baselines 
w[i,1,1] <- 0 # multi-arm adjustment = 0 for Rx1 
delta[i,1,1] <- 0 # treatment effect is 0 for Rx1 
pooled.SD.n[i,1] <- sum(SMD.SD.n[i,1:NumArms[i],1]) # sum SMD numerators 
pooled.SD.d[i,1] <- sum(SMD.SD.d[i,1:NumArms[i],1]) # sum SMD denominators 
pooled.SD[i,1] <- sqrt(pooled.SD.n[i,1] / pooled.SD.d[i,1]) 
# pooled SD across all arms 
for (j in 1:NumArms[i]) { # indexes arms 
MC[i,j,1] ~ dnorm(phi[i,j,1], prec[i,j,1]) # normal likelihood 
se[i,j,1] <- SD[i,j,1] / sqrt(N[i,j,1]) # set SEs 
var[i,j,1] <- pow(se[i,j,1], 2) # set variances 
prec[i,j,1] <- 1/var[i,j,1] # set precisions 
SMD.SD.d[i,j,1] <- N[i,j,1]-1 # pooled SD denom contribution 
SMD.SD.n[i,j,1] <- SMD.SD.d[i,j,1] * pow(SD[i,j,1],2) 
# pooled SD num contribution 
phi[i,j,1] <- theta[i,j,1] * (pooled.SD[i,1] * blnSMD + (1 - blnSMD)) 
# convert to SMD (if desired) 
theta[i,j,1] <- mu[i,1] 
+ delta[i,j,1] 
+ beta.PRN[1] * (PRN[i,j,1] - PRN[i,1,1]) 
+ beta.TREX[1] * (TREX[i,j,1] - TREX[i,1,1]) 
+ beta.PRNX[1] * (PRNX[i,j,1] - PRNX[i,1,1]) 
+ beta.Load[1] * (Load[i,j,1]*PRN[i,j,1] - Load[i,1,1]*PRN[i,1,1]) 
+ (beta.Freq[betaID[Rx[i,j,1]],1] * Freq[i,j,1]) 
- (beta.Freq[betaID[Rx[i,1,1]],1] * Freq[i,1,1]) 
# linear predictor with covariates 
dev[i,j] <- (MC[i,j,1] - phi[i,j,1]) * (MC[i,j,1] - phi[i,j,1]) * prec[i,j,1] 
# deviance contribution 
} # close arm loop 
for (j in 2:NumArms[i]) { # indexes arms 
taud[i,j,1] <- tau[1] *2*(j-1)/j # precision of MD dists, with MAC 
delta[i,j,1] ~ dnorm(md[i,j,1], taud[i,j,1]) # trial-specific MD distributions 
md[i,j,1] <- d[Rx[i,j,1],1] - d[Rx[i,1,1],1] + sw[i,j,1] 
# mean of MD dists, with MAC 
w[i,j,1] <- (delta[i,j,1] - d[Rx[i,j,1],1] + d[Rx[i,1,1],1]) 
# multi-arm correction (“MAC”) 
sw[i,j,1] <- sum(w[i,1:j-1,1])/(j-1) # cumulative MAC 
} # close arm loop 
resdev[i] <- sum(dev[i,1:NumArms[i]]) # trial-level deviance contribution 
} # close study loop
for(i in NumStudies.0_12only+1:NumStudies) { # indexes studies with 0-24 data 
for (k in 1:2) { # indexes timepoints 
mu[i,k] ~ dnorm(0, .0001) # vague priors for trial baselines 
w[i,1,1+(k-1)*2] <- 0 # multi-arm adjustment = 0 for Rx1 
delta[i,1,1+(k-1)*2] <- 0 # treatment effect is 0 for Rx1 
pooled.SD.n[i,k] <- sum(SMD.SD.n[i,1:NumArms[i],k]) # sum SMD numerators 
pooled.SD.d[i,k] <- sum(SMD.SD.d[i,1:NumArms[i],k]) # sum SMD denominators 
pooled.SD[i,k] <- sqrt(pooled.SD.n[i,k] / pooled.SD.d[i,k]) 
# pooled SD across all arms 
} # close timepoint loop 
mu[i,3] <- mu[i,2] - mu[i,1] # baseline for (1,2) is (0,2)-(0,1) 
for (j in 1:NumArms[i]) { # indexes arms 
MC[i,j,1:2] ~ dmnorm(phi[i,j,1:2], mvnPrec[i,j,,]) # mvnormal likelihood 
vcov[i,j,1,1] <- var[i,j,1] # vcov[1,1] 
vcov[i,j,2,1] <- var[i,j,1] # vcov[2,1] 
vcov[i,j,1,2] <- var[i,j,1] # vcov[1,2] 
vcov[i,j,2,2] <- var[i,j,2] # vcov[2,2] 
mvnPrec[i,j,1:2,1:2] <- inverse(vcov[i,j,,]) # convert vcov matrix to precision 
for (k in 1:2) { # indexes timepoints 
se[i,j,k] <- SD[i,j,k] / sqrt(N[i,j,k]) # set SEs 
var[i,j,k] <- pow(se[i,j,k], 2) # set variances 
prec[i,j,k] <- 1/var[i,j,k] # set precisions 
SMD.SD.d[i,j,k] <- N[i,j,k]-1 # pooled SD denom contribution 
SMD.SD.n[i,j,k] <- SMD.SD.d[i,j,k] * pow(SD[i,j,k],2) 
# pooled SD num contribution 
phi[i,j,k] <- theta[i,j,k] * (pooled.SD[i,k] * blnSMD + (1 - blnSMD)) 
# convert to SMD (if desired) 
theta[i,j,1+(k-1)*2] <- mu[i,1+(k-1)*2] 
+ delta[i,j,1+(k-1)*2] 
+ beta.PRN[1+(k-1)*2] 
* (PRN[i,j,1+(k-1)*2] - PRN[i,1,1+(k-1)*2]) 
+ beta.TREX[1+(k-1)*2] 
* (TREX[i,j,1+(k-1)*2] - TREX[i,1,1+(k-1)*2]) 
+ beta.PRNX[1+(k-1)*2] 
* (PRNX[i,j,1+(k-1)*2] - PRNX[i,1,1+(k-1)*2]) 
+ beta.Load[1+(k-1)*2] 
* (Load[i,j,1+(k-1)*2]*PRN[i,j,1+(k-1)*2] 
- Load[i,1,1+(k-1)*2]*PRN[i,1,1+(k-1)*2]) 
+ (beta.Freq[betaID[Rx[i,j,1+(k-1)*2]],1+(k-1)*2] 
* Freq[i,j,1+(k-1)*2]) 
- (beta.Freq[betaID[Rx[i,1,1+(k-1)*2]],1+(k-1)*2] 
* Freq[i,1,1+(k-1)*2]) # linear predictor with covariates 
} # close timepoint loop 
delta[i,j,2] <- delta[i,j,1] + delta[i,j,3] # sum yr1 effect and yr2 change 
theta[i,j,2] <- theta[i,j,1] + theta[i,j,3] # theta for (0,2) is (0,1)+(1,2) 
dev[i,j] <- mvnPrec[i,j,1,1]*pow(MC[i,j,1] - phi[i,j,1],2) 
+ mvnPrec[i,j,2,2]*pow(MC[i,j,2] - phi[i,j,2],2) 
+ 2*mvnPrec[i,j,1,2]*(MC[i,j,1] - phi[i,j,1])*(MC[i,j,2] - phi[i,j,2]) 
# deviance contribution 
} # close arm loop 
for (j in 2:NumArms[i]) { # indexes arms 
for (k in 1:2) { # indexes timepoints 
taud[i,j,1+(k-1)*2] <- tau[1+(k-1)*2]*2*(j-1)/j # precision of MD dists, with MAC 
md[i,j,1+(k-1)*2] <- d[Rx[i,j,1+(k-1)*2],1+(k-1)*2] 
- d[Rx[i,1,1+(k-1)*2],1+(k-1)*2] 
+ sw[i,j,1+(k-1)*2] # mean of MD dists, with MAC 
w[i,j,1+(k-1)*2] <- delta[i,j,1+(k-1)*2] 
- d[Rx[i,j,1+(k-1)*2],1+(k-1)*2] 
+ d[Rx[i,1,1+(k-1)*2],1+(k-1)*2] 
# multi-arm correction (“MAC”) 
sw[i,j,1+(k-1)*2] <- sum(w[i,1:j-1,1+(k-1)*2])/(j-1) 
# cumulative MAC 
} # close timepoint loop 
delta[i,j,1] ~ dnorm(md[i,j,1], taud[i,j,1]) # trial-specific MD distributions 
delta[i,j,3] ~ dnorm(md[i,j,3], taud[i,j,3]) # trial-specific MD distributions 
} # close arm loop 
resdev[i] <- sum(dev[i,1:NumArms[i]]) # trial-level deviance contribution 
} # close 0-24 study loop 
totresdev <- sum(resdev[]) # total residual deviance
# priors 
for (k in 1:2) { # indexes timepoints 
d[1,1+(k-1)*2] <- 0 # effect is 0 for Rx1 
for (j in 2:NumRx) { # indexes treatments 
d.prior[j,1+(k-1)*2] ~ dnorm(0, .0001) # vague priors, treatment effects 
d[j,1+(k-1)*2] <- d.prior[j,1+(k-1)*2] * nRx[j,1+(k-1)*2] 
# set effect to 0 if no evidence 
} # close treatment loop 
sdu[1+(k-1)*2] ~ dunif(RFXpriorParam1, RFXpriorParam2) # uniform between-trial prior 
sdn[1+(k-1)*2] ~ dnorm(RFXpriorParam1, RFXpriorParam2) # normal between-trial prior 
sdl[1+(k-1)*2] ~ dlnorm(RFXpriorParam1, RFXpriorParam2) # lognormal between-trial prior 
sd[1+(k-1)*2] <- sdu[1+(k-1)*2] * equals(RFXpriorD,1) 
+ sdn[1+(k-1)*2] * equals(RFXpriorD,2) 
+ sdl[1+(k-1)*2] * equals(RFXpriorD,3) # choose desired prior 
tau[1+(k-1)*2] <- pow(sd[1+(k-1)*2],-2) # between-trial precision 
b.PRN[1+(k-1)*2] ~ dnorm(0, .001) # prior for PRN coefficient 
b.Load[1+(k-1)*2] ~ dnorm(0, .001) # prior for loading coefficient 
b.PRNX[1+(k-1)*2] ~ dnorm(0, .001) # prior for PRNX coefficient 
b.TREX[1+(k-1)*2] ~ dnorm(0, .001) # prior for TREX coefficient 
beta.PRN[1+(k-1)*2] <- b.PRN[1+(k-1)*2] 
* blnCovars[1] * nCo[1,1+(k-1)*2] # ‘turn off’ if no data 
beta.Load[1+(k-1)*2] <- b.Load[1+(k-1)*2] 
* blnCovars[2] * nCo[2,1+(k-1)*2] # ‘turn off’ if no data 
beta.PRNX[1+(k-1)*2] <- b.PRNX[1+(k-1)*2] 
* blnCovars[3] * nCo[3,1+(k-1)*2] # ‘turn off’ if no data 
beta.TREX[1+(k-1)*2] <- b.TREX[1+(k-1)*2] 
* blnCovars[3] * nCo[4,1+(k-1)*2] # ‘turn off’ if no data 
for (i in 1:4) { 
b.Freq[i,1+(k-1)*2] ~ dnorm(0, .001) # priors for freq--response coefs 
beta.Freq[i,1+(k-1)*2] <- b.Freq[i,1+(k-1)*2] * blnCovars[4] 
* step(i-2) 
* nCo[5,1+(k-1)*2] # ‘turn off’ if ID=1 or no data 
} 
} 
beta.PRN[2] <- (beta.PRN[1] + beta.PRN[3]) * nCo[1,2] # beta(0,2) = (0,1)+(1,2) 
beta.Load[2] <- (beta.Load[1] + beta.Load[3]) * nCo[2,2] # beta(0,2) = (0,1)+(1,2) 
beta.PRNX[2] <- (beta.PRNX[1] + beta.PRNX[3]) * nCo[3,2] # beta(0,2) = (0,1)+(1,2) 
beta.TREX[2] <- (beta.TREX[1] + beta.TREX[3]) * nCo[4,2] # beta(0,2) = (0,1)+(1,2) 
for (i in 1:4) { 
beta.Freq[i,2] <- (beta.Freq[i,1] + beta.Freq[i,3]) 
* nCo[5,2] # beta(0,2) = (0,1)+(1,2) 
}
# fit effect estimates without and with covariate effects 
for (k in 1:3) { 
for (j in 1:NumRx) { 
d.fit[j,k] <- d[j,k] 
} 
for (c in 1:NumCovars) { 
for (i in 1:NumCore) { 
d.fit[NumRx+(c-1)*NumCore+i, k] <- d[core[i], k] 
+ beta.PRN[k] * equals(c, 1) 
+ beta.PRN[k] * equals(c, 2) 
+ beta.Load[k] * equals(c, 2) 
+ beta.TREX[k] * equals(c, 3) 
+ beta.PRN[k] * equals(c, 4) 
+ beta.Load[k] * equals(c, 4) 
+ beta.PRNX[k] * equals(c, 4) 
+ beta.Freq[betaID[core[i]], k] * equals(c, 5) * 1 
+ beta.Freq[betaID[core[i]], k] * equals(c, 6) * 2 
} 
} 
}
# generate final ‘d’s (set to null where no evidence) 
for (j in 1:NumRx) { 
d[j,2] <- d[j,1] + d[j,3] 
d.final[j,1] <- d.fit[j,1] * nRx[j,1] 
nRxCo[j,1] <- nRx[j,1] 
for (k in 2:3) { 
nRxCo[j,k] <- nRx[j,3] 
d.final[j,k] <- d.fit[j,k] * nRx[j,3] 
} 
} 
for (c in 1:NumCovars) { 
for (i in 1:NumCore) { 
for (k in 1:3) { 
nRxCo[NumRx+(c-1)*NumCore+i,k] <- nRx[core[i],k] * nCo[c,k] 
d.final[NumRx+(c-1)*NumCore+i,k] <- d.fit[NumRx+(c-1)*NumCore+i,k] 
* nRxCo[NumRx+(c-1)*NumCore+i,k] 
} 
} 
}
# Estimates of absolute treatment effects, given baseline 
for (k in 1:2) { 
precA[k] <- pow(SDA[k], -2) 
predPrecA[k] <- pow(predSDA[k], -2) 
AMean[k] ~ dnorm(meanA[k], precA[k]) 
APred[k] ~ dnorm(predA[k], predPrecA[k]) 
} 
Tmean[1,1] <- AMean[1] * (ASMD.SD[1] * blnSMD + (1-blnSMD)) 
Tmean[1,2] <- AMean[2] * (ASMD.SD[2] * blnSMD + (1-blnSMD)) 
Tpred[1,1] <- AMean[1] * (ASMD.SD[1] * blnSMD + (1-blnSMD)) 
Tpred[1,2] <- AMean[2] * (ASMD.SD[2] * blnSMD + (1-blnSMD)) 
Tmean[1,3] <- Tmean[1,2] - Tmean[1,1] 
Tpred[1,3] <- Tpred[1,2] - Tpred[1,1] 
for (j in 2:NumRx+NumCore*NumCovars) { 
for (k in 1:2) { 
Tmean[j,k] <- AMean[k] * (1-equals(d.final[j,k], 0)) 
+ d.final[j,k] * (ASMD.SD[k] * blnSMD + (1-blnSMD)) 
Tpred[j,k] <- APred[k] * (1-equals(d.final[j,k], 0)) 
+ d.final[j,k] * (ASMD.SD[k] * blnSMD + (1-blnSMD)) 
} 
Tmean[j,3] <- (Tmean[j,2] - Tmean[j,1]) * (1-equals(d.final[j,2], 0)) 
Tpred[j,3] <- (Tpred[j,2] - Tpred[j,1]) * (1-equals(d.final[j,2], 0)) 
}
for (k in 1:3) { 
# pairwise MDs for all possible pair-wise comparisons 
for (c in 1:(NumRx+NumCore*NumCovars-1)) { 
for (j in (c+1):NumRx+NumCore*NumCovars) { 
MD[c,j,k] <- (d.final[j,k] - d.final[c,k]) * nRxCo[j,k] * nRxCo[c,k] 
} 
}
# ranking on relative scale 
for (j in 1:NumRx+NumCore*NumCovars) { 
rk[j,k] <- blnHiGood*(NumRx+NumCore*NumCovars+1-rank(d.toRank[,k],j)) 
+ (1-blnHiGood)*rank(d.toRank[,k],j) 
best[j,k] <- equals(rk[j,k],1) # prob. that treat j is best 
for (h in 1:NumRx+NumCore*NumCovars) { 
pRk[h,j,k] <- equals(rk[j,k],h) # prob. that treat j is hth best 
} 
} 
}
# values for ranking (set to -999 if no evidence) 
for (c in 1:NumRx) { 
d.toRank[c,1] <- d.final[c,1] + (1-nRx[c,1])*-999 
for (k in 2:3) { 
d.toRank[c,k] <- d.final[c,k] + (1-nRx[c,3])*-999 
} 
} 
for (k in 1:3) { 
for (c in 1:NumCovars) { 
for (i in 1:NumCore) { 
d.toRank[NumRx+(c-1)*NumCore+i,k] <- d.final[NumRx+(c-1)*NumCore+i,k] * nCo[c,k] 
+ (1-nCo[c,k])*-999 
} 
} 
}
# establish which treatments have evidence 
for (l in 1:NumRx) { 
for (i in 1:NumStudies) { 
for (j in 1:NumArms[i]) { 
nnnRx[l,i,j,1] <- equals(Rx[i,j,1], l) 
} 
nnRx[l,i,1] <- sum(nnnRx[l,i,1:NumArms[i],1]) 
} 
for (i in NumStudies.0_12only+1:NumStudies) { 
for (j in 1:NumArms[i]) { 
nnnRx[l,i,j,3] <- equals(Rx[i,j,3], l) 
} 
nnRx[l,i,3] <- sum(nnnRx[l,i,1:NumArms[i],3]) 
} 
nRx[l,1] <- step(sum(nnRx[l,1:NumStudies,1])-1) 
nRx[l,3] <- step(sum(nnRx[l,NumStudies.0_12only+1:NumStudies,3])-1) 
nRx[l,2] <- nRx[l,1] * nRx[l,3] 
}
# establish which covariates have evidence 
for (i in 1:NumStudies.0_12only) { 
for (j in 1:NumArms[i]) { 
nnnCo[i,j,1,1] <- step(PRN[i,j,1]-1) 
nnnCo[i,j,2,1] <- step(Load[i,j,1]-1) 
nnnCo[i,j,3,1] <- step(TREX[i,j,1]-1) 
nnnCo[i,j,4,1] <- step(PRNX[i,j,1]-1) 
nnnCo[i,j,5,1] <- step(Freq[i,j,1]-1.01) 
nnnCo[i,j,6,1] <- step(Freq[i,j,1]-1.01) 
} 
for (c in 1:6) { 
nnCo[i,c,1] <- sum(nnnCo[i,1:NumArms[i],c,1]) 
nnCo[i,c,3] <- 0 
} 
} 
for (i in NumStudies.0_12only+1:NumStudies) { 
for (k in 1:2) { 
for (j in 1:NumArms[i]) { 
nnnCo[i,j,1,1+(k-1)*2] <- step(PRN[i,j,1+(k-1)*2]-1) 
nnnCo[i,j,2,1+(k-1)*2] <- step(Load[i,j,1+(k-1)*2]-1) 
nnnCo[i,j,3,1+(k-1)*2] <- step(TREX[i,j,1+(k-1)*2]-1) * equals(k, 1) 
nnnCo[i,j,4,1+(k-1)*2] <- step(PRNX[i,j,1+(k-1)*2]-1) * equals(k, 1) 
nnnCo[i,j,5,1+(k-1)*2] <- step(Freq[i,j,1+(k-1)*2]-1.01) 
nnnCo[i,j,6,1+(k-1)*2] <- step(Freq[i,j,1+(k-1)*2]-1.01) 
} 
for (c in 1:6) { 
nnCo[i,c,1+(k-1)*2] <- sum(nnnCo[i,1:NumArms[i],c,1+(k-1)*2]) 
} 
} 
} 
for (c in 1:6) { 
nCo[c,1] <- step(sum(nnCo[1:NumStudies,c,1])-1) 
nCo[c,3] <- step(sum(nnCo[NumStudies.0_12only+1:NumStudies,c,3])-1) 
nCo[c,2] <- nCo[c,1] * nCo[c,3] 
} 
nnCo[1,1,99] <- 0 # dummy data to stop BUGS tripping over when numCovars == 0 
nCo[1,99] <- 0 # dummy data to stop BUGS tripping over when numCovars == 0 
}

G.4.1.2. Categorical data

Binomial model with probit link, with provision for meta-regression (inter-study random effects; inter-category random effects)

# Binomial likelihood, probit link (ordered categorical data) 
# Fixed effects model for multi-arm trials 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Sutton, A.J., Welton, N.J. & Ades, A.E. 
# NICE DSU Technical Support Document 3: Heterogeneity: subgroups, meta-regression, 
# bias and bias-adjustment. 2011; last updated April 2012. 
# http://www.nicedsu.org.uk 
# 
# This model will include covariates if numCovars is set to > 1 and blnCovars != c(0,0,0,0) 
# blnCovars[1] is a switch for PRN 
# blnCovars[2] is a switch for Load 
# blnCovars[3] is a switch for TREX and PRNX 
# blnCovars[4] is a switch for Frequency 
# Outputs are calculated with and without covariates for treatments identifed in core c()
model { 
for(i in 1:NumStudies) { # indexes studies 
w[i,1] <- 0 # multi-arm adjustment =0 for control arm 
delta[i,1] <- 0 # treatment effect =0 for control arm 
mu[i] ~ dnorm(0, .0001) # vague priors for all trial baselines 
zeta[i,1] <- 0 # z-score is 0 for bottom category 
for (c in 2:maxNumCats-1) { # indexes categories in trial 
zeta.sd[i,c] <- sqrt(log(1+(pow(z.sd,2)/pow(z.aux[c],2)))) 
# calculate SD of lognorm dist 
zeta.mean[i,c] <- log(z.aux[c]) - 0.5 * pow(zeta.sd[i,c],2) 
# calculate mean of lognorm dist 
zeta.prec[i,c] <- pow(zeta.sd[i,c],-2) # convert SD to precision 
zeta.aux[i,c] ~ dlnorm(zeta.mean[i,c], zeta.prec[i,c]) 
# interval between z-scores 
zeta[i,c] <- zeta[i,c-1] + zeta.aux[i,c] 
# add interval to prev z-score to get new one 
} # close category loop 
for (j in 1:NumArms[i]) { # indexes arms 
p[i,j,1] <- 1 # Pr(score>0 = 1) 
for (c in 1:numCats[i]-1) { # indexes categories 
n[i,j,c] <- N[i,j] - sum(r[i,j,1:c]) + r[i,j,c] 
r[i,j,c] ~ dbin(q[i,j,c], n[i,j,c]) # binomial likelihood 
q[i,j,c] <- 1-(p[i,j,C[i,c+1]]/p[i,j,C[i,c]]) 
# conditional probabilities 
theta[i,j,c] <- mu[i] 
+ delta[i,j] 
+ zeta[i,C[i,c+1]-1] 
+ beta.PRN * (PRN[i,j] - PRN[i,1]) 
+ beta.Load * (Load[i,j]*PRN[i,j] - Load[i,1]*PRN[i,1]) 
+ beta.TREX * (TREX[i,j] - TREX[i,1]) 
+ beta.PRNX * (PRNX[i,j] - PRNX[i,1]) 
+ (beta.Freq[betaID[Rx[i,j]]] * Freq[i,j]) 
- (beta.Freq[betaID[Rx[i,1]]] * Freq[i,1]) 
# linear predictor 
rhat[i,j,c] <- q[i,j,c] * n[i,j,c] # predicted number events 
dv[i,j,c] <- 2 * (r[i,j,c]*(log(r[i,j,c]) - log(rhat[i,j,c])) 
+(n[i,j,c] - r[i,j,c]) * (log(n[i,j,c]-r[i,j,c]) 
- log(n[i,j,c] - rhat[i,j,c]))) 
# deviance contribution 
} # close category loop 
dev[i,j] <- sum(dv[i,j,1:numCats[i]-1]) # deviance contribution of each arm 
for (c in 2:numCats[i]) { # indexes categories 
p[i,j,C[i,c]] <- 1 - phi(theta.adj[i,j,c]) 
# link function 
theta.adj[i,j,c] <- step(-5-theta[i,j,c-1]) * -5 
+ step(theta[i,j,c-1]-5) * 5 
+ step(5-theta[i,j,c-1]) * step(theta[i,j,c-1]+5) 
* theta[i,j,c-1] # adjust phi(x) for values that can give 
# numerical errors when x< -5, phi(x)=0, 
# when x> 5, phi(x)=1 
} # close category loop 
} # close arm loop 
for (j in 2:NumArms[i]) { # indexes arms 
delta[i,j] ~ dnorm(md[i,j], taud[i,j]) # trial-specific MD distributions 
md[i,j] <- d[Rx[i,j]] - d[Rx[i,1]] + sw[i,j] 
# mean of MD dists, with MAC 
taud[i,j] <- tau * 2 * (j-1) / j # precision of MD dists, with MAC 
w[i,j] <- (delta[i,j] - d[Rx[i,j]] + d[Rx[i,1]]) # adjustment, multi-arm RCTs 
# multi-arm correction (“MAC”) 
sw[i,j] <- sum(w[i,1:j-1]) / (j-1) # cumulative MAC 
} # close arm loop 
resdev[i] <- sum(dev[i,1:NumArms[i]]) # summed residual deviance for this trial 
} # close trial loop 
totresdev <- sum(resdev[]) # total residual deviance
z[1] <- 0 # set z=0 for bottom category 
for (j in 2:maxNumCats-1) { # indexes all categories 
z.aux[j] ~ dunif(0,5) # vague priors for inter-categories intervals 
z[j] <- z[j-1] + z.aux[j] # z-score = prev z-score plus interval 
} # close category loop 
z.sd ~ dunif(0, 2) # vague prior for between-trial z SD 
z.prec <- pow(z.sd, -2) # between-trial z precision
d[1] <- 0 # effect is zero for reference treatment 
for (j in 2:NumRx) { # indexes treatments 
d[j] ~ dnorm(0, .0001) # vague priors for treatment effects 
} 
sdu ~ dunif(RFXpriorParam1, RFXpriorParam2) # uniform between-trial prior 
sdn ~ dnorm(RFXpriorParam1, RFXpriorParam2) # normal between-trial prior 
sdl ~ dlnorm(RFXpriorParam1, RFXpriorParam2) # lognormal between-trial prior 
sd <- sdu * equals(RFXpriorD,1) 
+ sdn * equals(RFXpriorD,2) 
+ sdl * equals(RFXpriorD,3) # choose desired between-trial prior 
tau <- pow(sd, -2) # between-trial precision
# covariates 
b.PRN ~ dnorm(0, .001) 
b.Load ~ dnorm(0, .001) 
b.TREX ~ dnorm(0, .001) 
b.PRNX ~ dnorm(0, .001) 
beta.PRN <- b.PRN * blnCovars[1] 
beta.Load <- b.Load * blnCovars[2] 
beta.TREX <- b.TREX * blnCovars[3] 
beta.PRNX <- b.PRNX * blnCovars[3] 
beta.Freq[1] <- 0 
for (i in 2:3) { 
b.Freq[i] ~ dnorm(0, .001) 
beta.Freq[i] <- b.Freq[i] * blnCovars[4] 
} 
# hardcoded IDs for frequency covariates 
betaID[1] <- 3 
betaID[2] <- 1 
betaID[3] <- 1 
betaID[4] <- 2 
betaID[5] <- 3 
betaID[6] <- 1 
betaID[7] <- 1
#effect estimates without and with covariate effects 
for (c in 1:NumRx) { 
dd[c] <- d[c] 
} 
for (c in 1:NumCovars) { 
for (i in 1:NumCore) { 
dd[NumRx+(c-1)*NumCore+i] <- d[core[i]] 
+ beta.PRN * equals(c, 1) 
+ beta.PRN * equals(c, 2) 
+ beta.Load * equals(c, 2) 
+ beta.TREX * equals(c, 3) 
+ beta.PRN * equals(c, 4) 
+ beta.Load * equals(c, 4) 
+ beta.PRNX * equals(c, 4) 
+ beta.Freq[betaID[core[i]]] * equals(c, 5) * 1 
+ beta.Freq[betaID[core[i]]] * equals(c, 6) * 2 
} 
}
# Provide estimates of treatment effects T[j] on the natural (probability) scale 
precA <- pow(SDA, -2) 
predPrecA <- pow(predSDA, -2) 
AMean ~ dnorm(meanA, precA) 
APred ~ dnorm(predA, predPrecA) 
for (i in 1:(NumRx+NumCore*NumCovars)) { 
for (j in 1:maxNumCats-1) { 
Tmean[i,j] <- 1 - phi(AMean + dd[i] + z[j]) 
Tpred[i,j] <- 1 - phi(APred + dd[i] + z[j]) 
} 
}
# pairwise z-scores for all possible pair-wise comparisons 
for (i in 1:((NumRx+NumCore*NumCovars)-1)) { 
for (j in (i+1):NumRx+NumCore*NumCovars) { 
pairZ[i,j] <- dd[j] - dd[i] 
} 
}
# ranking on relative scale 
for (j in 1:NumRx+NumCore*NumCovars) { 
rk[j] <- blnHiGood*(NumRx+NumCore*NumCovars+1-rank(dd[],j)) 
+ (1-blnHiGood)*rank(dd[],j) 
best[j] <- equals(rk[j],1) # prob that treat j is best 
for (h in 1:NumRx+NumCore*NumCovars) { 
pRk[h,j] <- equals(rk[j],h) # prob that treat j is hth best 
} 
} 
} # *** PROGRAM ENDS

G.4.1.3. Dichotomous data

Binomial model with logit link, with provision for meta-regression (random effects)

# Binomial likelihood, logit link 
# Random-effects model for multi-arm trials 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Sutton, A.J., Welton, N.J. & Ades, A.E. 
# NICE DSU Technical Support Document 3: Heterogeneity: subgroups, meta-regression, 
# bias and bias-adjustment. 2011; last updated April 2012. 
# http://www.nicedsu.org.uk 
# 
# This model will include covariates if numCovars is set to > 1 and blnCovars != c(0,0,0,0) 
# blnCovars[1] is a switch for PRN 
# blnCovars[2] is a switch for Load 
# blnCovars[3] is a switch for TREX and PRNX 
# blnCovars[4] is a switch for Frequency 
# Outputs are calculated with and without covariates for treatments identifed in core c()
model { 
for(i in 1:NumStudies) { # indexes studies 
mu[i] ~ dnorm(0, .0001) # vague priors for all trial baselines 
delta[i,1] <- 0 # effect is zero for control arm 
w[i,1] <- 0 # multi-arm adjustment = zero for ctrl 
for (j in 1:NumArms[i]) { # indexes arms 
k[i,j] ~ dbin(p[i,j],N[i,j]) # binomial likelihood 
logit(p[i,j]) <- mu[i] 
+ delta[i,j] 
+ beta.PRN * (PRN[i,j] - PRN[i,1]) 
+ beta.TREX * (TREX[i,j] - TREX[i,1]) 
+ beta.PRNX * (PRNX[i,j] - PRNX[i,1]) 
+ beta.Load * (Load[i,j]*PRN[i,j] - Load[i,1]*PRN[i,1]) 
+ (beta.Freq[betaID[Rx[i,j]]] * Freq[i,j]) 
- (beta.Freq[betaID[Rx[i,1]]] * Freq[i,1]) 
# linear predictor with covariates 
rhat[i,j] <- p[i,j] * N[i,j] # expected value of the numerators 
dev[i,j] <- 2 * (k[i,j] * (log(k[i,j])-log(rhat[i,j])) 
+ (N[i,j]-k[i,j]) * (log(N[i,j]-k[i,j]) - log(N[i,j]-rhat[i,j]))) 
# deviance contribution 
} # close arm loop 
for (j in 2:NumArms[i]) { # indexes arms 
delta[i,j] ~ dnorm(md[i,j],taud[i,j]) # trial-specific LOR distributions 
md[i,j] <- d[Rx[i,j]] - d[Rx[i,1]] + sw[i,j] # mean of LOR distributions (with MAC)) 
taud[i,j] <- tau *2*(j-1)/j # precision of LOR distributions (with MAC) 
w[i,j] <- (delta[i,j] - d[Rx[i,j]] + d[Rx[i,1]]) 
# multi-arm correction (“MAC”) 
sw[i,j] <- sum(w[i,1:j-1])/(j-1) # cumulative MAC 
} # close arm loop 
resdev[i] <- sum(dev[i,1:NumArms[i]]) # summed deviance contribution 
} # close study loop 
totresdev <- sum(resdev[]) # total residual deviance
d[1]<-0 # effect is 0 for reference treatment 
for (j in 2:NumRx) { # indexes treatments 
d[j] ~ dnorm(0, .0001) # vague priors for treatment effects 
} # close treatment loop 
sdu ~ dunif(RFXpriorParam1, RFXpriorParam2) # uniform between-trial prior 
sdn ~ dnorm(RFXpriorParam1, RFXpriorParam2) # normal between-trial prior 
sdl ~ dlnorm(RFXpriorParam1, RFXpriorParam2) # lognormal between-trial prior 
sd <- sdu * equals(RFXpriorD,1) 
+ sdn * equals(RFXpriorD,2) 
+ sdl * equals(RFXpriorD,3) # select correct between-trial prior 
tau <- pow(sd,-2) # between-trial precision
# covariates 
b.PRN ~ dnorm(0, .001) 
b.Load ~ dnorm(0, .001) 
b.TREX ~ dnorm(0, .001) 
b.PRNX ~ dnorm(0, .001) 
beta.PRN <- b.PRN * blnCovars[1] 
beta.Load <- b.Load * blnCovars[2] 
beta.TREX <- b.TREX * blnCovars[3] 
beta.PRNX <- b.PRNX * blnCovars[3] 
beta.Freq[1] <- 0 
for (i in 2:3) { 
b.Freq[i] ~ dnorm(0, .001) 
beta.Freq[i] <- b.Freq[i] * blnCovars[4] 
} 
# hardcoded IDs for frequency covariates 
betaID[1] <- 3 
betaID[2] <- 1 
betaID[3] <- 1 
betaID[4] <- 2 
betaID[5] <- 3 
betaID[6] <- 1 
betaID[7] <- 1
#effect estimates without and with covariate effects 
for (c in 1:NumRx) { 
dd[c] <- d[c] 
} 
for (c in 1:NumCovars) { 
for (i in 1:NumCore) { 
dd[NumRx+(c-1)*NumCore+i] <- d[core[i]] 
+ beta.PRN * equals(c, 1) 
+ beta.PRN * equals(c, 2) 
+ beta.Load * equals(c, 2) 
+ beta.TREX * equals(c, 3) 
+ beta.PRN * equals(c, 4) 
+ beta.Load * equals(c, 4) 
+ beta.PRNX * equals(c, 4) 
+ beta.Freq[betaID[core[i]]] * equals(c, 5) * 1 
+ beta.Freq[betaID[core[i]]] * equals(c, 6) * 2 
} 
}
# Provide estimates of treatment effects T[j] on the natural (probability) scale 
precA <- pow(SDA, -2) 
predPrecA <- pow(predSDA, -2) 
AMean ~ dnorm(meanA, precA) 
APred ~ dnorm(predA, predPrecA) 
for (j in 1:(NumRx+NumCore*NumCovars)) { 
logit(Tmean[j]) <- AMean + dd[j] 
logit(Tpred[j]) <- APred + dd[j] 
}
# pairwise ORs and LORs for all possible pair-wise comparisons 
for (c in 1:((NumRx+NumCore*NumCovars)-1)) { 
for (j in (c+1):(NumRx+NumCore*NumCovars)) { 
lOR[c,j] <- (dd[j] - dd[c]) 
OR[c,j] <- exp(lOR[c,j]) 
} 
}
# ranking on relative scale 
for (j in 1:(NumRx+NumCore*NumCovars)) { 
rk[j] <- blnHiGood*((NumRx+NumCore*NumCovars)+1-rank(dd[],j)) + (1-blnHiGood)*rank(dd[],j) 
best[j] <- equals(rk[j],1) # probability that treat j is best 
for (h in 1:(NumRx+NumCore*NumCovars)) { 
pRk[h,j] <- equals(rk[j],h) # probability that treat j is hth best 
} 
} 
}

G.4.2. Baseline syntheses

G.4.2.1. Continuous data

Bivariate normal model for 1- and 2-year data (random effects)

# Baseline model for continuous data 
# multivariate normal likelihood, identity link 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 5: Evidence synthesis in the baseline 
# natural history model. 2011. 
# http://www.nicedsu.org.uk
model { 
for(i in 1:NumStudies.0_12only) { # indexes studies 
se[i,1] <- SD[i,1] / sqrt(N[i,1]) # calculate SEs 
prec[i] <- pow(se[i,1], -2) # set precisions 
mu[i,1] ~ dnorm(m[1], tau[1]) # trial-specific baseline with random effects 
MC[i,1] ~ dnorm(p[i], prec[i]) # normal likelihood 
p[i] <- mu[i,1] # identity link 
} 
for(i in NumStudies.0_12only+1:NumStudies) { # indexes studies with 0-24 data 
MC[i,1:2] ~ dmnorm(phi[i,1:2], mvnPrec[i,,]) # mvnormal likelihood 
vcov[i,1,1] <- var[i,1] # vcov[1,1] 
vcov[i,2,1] <- var[i,1] # vcov[2,1] 
vcov[i,1,2] <- var[i,1] # vcov[1,2] 
vcov[i,2,2] <- var[i,2] # vcov[2,2] 
mvnPrec[i,1:2,1:2] <- inverse(vcov[i,,]) # convert vcov matrix to precision 
for (k in 1:2) { # indexes timepoints 
se[i,k] <- SD[i,k] / sqrt(N[i,k]) # calculate SEs 
var[i,k] <- pow(se[i,k], 2) # set variances 
mu[i,k] ~ dnorm(m[k], tau[k]) # trial-specific baseline with random effects 
phi[i,k] <- mu[i,k] # identity link 
} 
} # close study loop 
for (k in 1:2) { 
sd[k] ~ dunif(0, 5) # vague prior for SD (baseline) 
tau[k] <- pow(sd[k], -2) # between-trial precision (baseline) 
m[k] ~ dnorm(0, .0001) # vague prior for mean (baseline) 
prob[k] <- m[k] # posterior mean 
mu.new[k] ~ dnorm(m[k], tau[k]) # pred. dist. for baseline 
pred[k] <- mu.new[k] # predictive mean for a new observation 
} 
}

G.4.2.2. Categorical data

Binomial model with probit link (inter-study random effects; inter-category random effects)

# Binomial likelihood, probit link (different categories) 
# Fixed-effects baseline model 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Welton, N.J., Sutton, A.J., Ades, A.E. 
# NICE DSU Technical Support Document 5: Evidence synthesis in the baseline 
# natural history model. 2011. 
# http://www.nicedsu.org.uk
model { 
for(i in 1:NumStudies) { # indexes studies 
mu[i] ~ dnorm(m, tau.m) # trial-specific baseline with random FX 
zeta[i,1] <- 0 # z-score is 0 for bottom category 
for (c in 2:maxNumCats-1) { # indexes categories in trial 
zeta.sd[i,c] <- sqrt(log(1+(pow(z.sd,2)/pow(z.aux[c],2)))) 
# calculate SD of lognorm dist 
zeta.mean[i,c] <- log(z.aux[c]) - 0.5 * pow(zeta.sd[i,c],2) 
# calculate mean of lognorm dist 
zeta.prec[i,c] <- pow(zeta.sd[i,c],-2) # convert SD to precision 
zeta.aux[i,c] ~ dlnorm(zeta.mean[i,c], zeta.prec[i,c]) 
# interval between z-scores 
zeta[i,c] <- zeta[i,c-1] + zeta.aux[i,c] 
# add interval to prev z-score to get new one 
} # close category loop 
p[i,1] <- 1 # Pr(score>0 = 1) 
for (c in 1:numCats[i]-1) { # indexes categories 
n[i,c] <- N[i] - sum(r[i,1:c]) + r[i,c] # calculate category-specific ns 
r[i,c] ~ dbin(q[i,c], n[i,c]) # binomial likelihood 
q[i,c] <- 1 - (p[i,C[i,c+1]] / p[i,C[i,c]]) 
# conditional probabilities 
theta[i,c] <- mu[i] + zeta[i,C[i,c+1]-1] # linear predictor 
} # close category loop 
for (c in 2:numCats[i]) { # indexes categories 
p[i,C[i,c]] <- 1 - phi(theta.adj[i,c]) # link function 
theta.adj[i,c] <- step(-5-theta[i,c-1]) * -5 
+ step(theta[i,c-1]-5) * 5 
+ step(5-theta[i,c-1]) * step(theta[i,c-1]+5) 
* theta[i,c-1] # adjust phi(x) for values that can give 
# numerical errors when x< -5, phi(x)=0, 
# when x> 5, phi(x)=1 
} # close category loop 
} # close study loop 
z[1] <- 0 # set z=0 for bottom category 
for (j in 2:maxNumCats-1) { # indexes all categories 
z.aux[j] ~ dunif(0,5) # vague priors for inter-categories intervals 
z[j] <- z[j-1] + z.aux[j] # z-score = prev z-score plus interval 
} # close category loop 
z.sd ~ dunif(0, 2) # vague prior for between-trial z SD 
z.prec <- pow(z.sd, -2) # between-trial z precision 
sd.m ~ dunif(0, 5) # vague prior for SD (baseline) 
tau.m <- pow(sd.m, -2) # between-trial precision (baseline) 
m ~ dnorm(0, .0001) # vague prior for mean (baseline) 
prob <- step(5+m) * (step(m-5) + step(5-m) * phi(m)) 
# posterior probability (response = cat1) 
mu.new ~ dnorm(m, tau.m) # pred. dist. for baseline (log-hazard) 
pred <- step(5+mu.new) * (step(mu.new-5) + step(5-mu.new) * phi(mu.new)) 
# predictive probability (response = cat1) 
}

G.4.2.3. Dichotomous data

Binomial model with logit link (random effects)

# Baseline model for dichotomous data 
# binomial likelihood, logit link 
# based on 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework 
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 
# 2011; last updated September 2016. 
# and 
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E. 
# NICE DSU Technical Support Document 5: Evidence synthesis in the baseline 
# natural history model. 2011. 
# http://www.nicedsu.org.uk
model { 
for(i in 1:NumStudies) { # indexes studies 
k[i] ~ dbin(p[i], N[i]) # binomial likelihood 
logit(p[i]) <- mu[i] # model for linear predictor 
mu[i] ~ dnorm(m, tau.m) # trial-specific baseline with random effects 
} # close study loop 
sd.m ~ dunif(0, 5) # vague prior for SD (baseline) 
tau.m <- pow(sd.m, -2) # between-trial precision (baseline) 
m ~ dnorm(0, .0001) # vague prior for mean (baseline) 
logit(prob) <- m # posterior probability of response 
mu.new ~ dnorm(m, tau.m) # pred. dist. for baseline (log-odds) 
logit(pred) <- mu.new # predictive probability of response 
}

NICE 2018

Acknowledgements

The syntheses described in this document were conceptualised and implemented with the invaluable advice of the NICE clinical guidelines technical support unit (Nicky Welton, Sofia Dias, Edna Keeney).

Sylwia Bujkiewicz provided some useful comments on the use of a multivariate likelihood in an NMA.

Any errors that remain are the responsibility of the developers and the guideline committee.

Footnotes

a: Academic-in-confidence data supplied by the manufacturer of aflibercept to TA294, used with consent for this analysis
b: Academic-in-confidence data supplied by the manufacturer of aflibercept to TA294, used with consent for this analysis

Bookshelf ID: NBK536480

Contents

< Prev Next >

PubReader
Print View
Cite this Page
Age-related macular degeneration: diagnosis and management. London: National Institute for Health and Care Excellence (NICE); 2018 Jan. (NICE Guideline, No. 82.) Appendix G, Network meta-analysis.
PDF version of this page (7.0M)
PDF version of this title (4.1M)

Other titles in this collection

National Institute for Health and Care Excellence: Guidelines

Related information

PMC
PubMed Central citations
PubMed
Links to PubMed

Recent Activity

Clear Turn Off Turn On

Network meta-analysis - Age-related macular degeneration
Network meta-analysis - Age-related macular degeneration

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on