Butterfly color patterns are built as finely tiles mosaics of colored scales, each the product of a single epidermal cell. The overall pattern is composed of a small number of pigments. Each scale appears to make an all-or-none “choice” to synthesize only one of this small set of alternative pigments. Gradual transitions from one color to another on the wing are accomplished by graded changes in the proportions of discretely colored scales, and areas of intermediate coloration are made up of a random salt-and-pepper mosaic of discretely colored scales. In transition regions, and at boundaries between colors, scales also exhibit stochastic patterns of pigment expression. A model for a stochastic mechanism for gene expression is presented that can account for the observed stochastic patterns of pigmentation. This model shows that stochastic gene expression provides a simple mechanism for establishing a step-like, or threshold, response to a spatially graded signal. Conditions that affect the steepness of the threshold are examined. It is shown that stochastic gene expression also results in the emergence of interesting patterns of dominance among the alleles of a gene.

Introduction

Stochastic gene expression occurs when transcriptional regulators are present at very low concentrations, so that binding and release of regulators from their binding sites becomes probabilistic. The suspicion that stochastic gene expression has a significant effect on the biology of organisms comes from the observation that genetically identical (clonal) organisms, maintained in identical environments, diverge phenotypically. For instance, cells division in bacteria growing in an optimum medium rapidly becomes asynchronous, presumably due to individual stochastic variation in regulatory processes.¹ Stochastic gene expression has been observed in artificial genetic constructs.² In addition, stochastic gene expression and has been suggested to be a significant cause of haploinsufficiency.³

We have found that stochastic gene expression is a common and easily observable feature in the development of butterfly color patterns. Color patterns are made up of pigmented scales; each scale is the outgrowth of a single epidermal cell, and typically contains only a single pigment. The overall color pattern is a pixellated mosaic of monochrome scales, and in most patterns each scale-cell makes an all-or-none decision to synthesize one of a small set of alternative pigments.

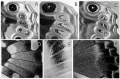
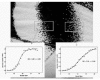
Stochastic genes expression occurs in four different ways in this mosaic. First, where alternative colors are controlled by allelic differences at a single gene and there is incomplete dominance, the color of the heterozygote is intermediate between that of the two homozygotes, and this is due, not to an intermediate amount of pigment, but due to the fact that a fraction of the scales develop one color and the remainder develop the other color (Fig. 1). Second, many natural color patterns are entirely made up of a random, salt-and-pepper arrangement of scales of two or three colors, often with gradations in color that are accomplished by spatial changes in the relative frequency of each of the colors (Fig. 2). Thirdly, stochastic gene expression occurs at the boundaries between two areas of solid color. Even the sharpest boundaries are noisy, with many scales expressing a color that is out of place. In many cases the boundaries are rather wide and exhibit a gradient in the frequency of the two adjoining colors (Fig. 3).

Figure 1

A cross of two genotypes of Papilio dardanus with codominant alleles. In many regions of the wing the heterozygote on the right has a pigmentation (gray) roughly intermediate between that of the parental types (black and white). The intermediate pigmentation (more...)

Figure 2

Closeup of the color pattern on the ventral hind wing of Morpho hecuba, illustrating stochastic pigmentation at boundaries between pattern and in certain regions of the color pattern.

Figure 3

Stochastic pigment expression is a common feature of butterfly color patterns. Top row shows individual variation of stochastic patterning in Lethe europa Other panels illustrate various manifestations of stochastic pigment expression that is part of (more...)

Finally, each pigment in the eyespot patterns of butterflies is preceded by the expression of a unique combination of transcription factors.⁴ In large areas of homogeneous color, the relevant transcription factors become expressed in all cells, but the initiation of expression is stochastic. Expression begins in a sparse random pattern of cells that gradually fills in until all cells in the field that will become that particular color express these genes.⁴ Thus the initial spatial pattern of gene activation in large areas of homogeneous gene expression is also stochastic.

The present paper is an exploration of the potential causes behind these various manifestations of stochastic gene expression. We take as our starting point a mathematical approach to understanding stochastic gene expression and use this to examine the conditions under which the observed patterns of stochastic expression in butterfly wings could occur. We will see that dominance is an emergent property of stochastic gene expression, due to the extreme nonlinearity of the relationship between transactivator concentration and the probability of gene expression.

A General Model of Stochastic Gene Expression

Stochastic gene expression is thought to be the consequence of the random activation and inactivation of transcription due to successive cycles of binding and release of a transcription factor.⁵ Activation and inactivation are assumed to occur by a first-order reversible reaction

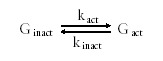
If the probability of gene activation is uniform overt time, then the time between activation events will have an exponential distribution given by the probability density function

f(t) = e^−t/b/b,       (1)

and the probability that an event has occurred is given by cumulative density function

F(t)= 1− e^−t/b,       (2)

where b is the mean time between events. Among the properties of an exponential distribution is that the standard deviation is the same as the mean, and the median time between events is the half-time of the reaction: t_1/2 = ln2*b = 0.693*b. If gene activation occurs as a first-order reaction

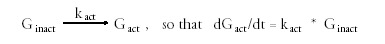
A gene becomes inactivated by (1) the removal of a transcriptional activator, or by (2) the binding of a transcriptional inhibitor. Like gene activation, these two kinds of inactivation events can also be stochastic. The effects of the two types of inactivation events are presumably independent of each other, so we assume that kinact is the sum of the stochastic rate of removal of the transcriptional activator and the stochastic rate of binding of a transcriptional inhibitor (k_inact = k_act-off + k_inh-on). The fraction of time a gene is active is given by k_act/(k_act+k_inact). This ratio also gives the fraction of cells in which a gene is active at any given time.

We follow ref. 3 in assuming that the activated gene produces a gene product (P) via a first-order mechanism, and that this product decays at a rate proportional to its concentration:

dP/dt = k₃*G_act − k₄*P.       (4)

In diploid individuals two genes (G₁ and G₂) contribute independently to the synthesis of product, so the rate becomes

dP/dt = k₃*(G_1act + G_2act) − k₄*P.       (5)

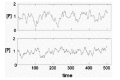
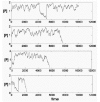
The concentration of the product P fluctuates with stochastic variation in G_act (Fig. 4A). The amplitude of the fluctuation in [P] is determined by the half-times of activation and inactivation of the gene and the rates of synthesis and destruction of P. If the half-time of activation/ inactivation is long (implying small k_act and k_inact) and the rates of P synthesis and decay are large, the fluctuations will be large. If the half-times of inactivation and inactivation are short (implying large k_act and k_inact) the fluctuation of P will have a smaller amplitude (Fig. 4B).

Figure 4

The rate constants of gene activation and inactivation affect the amplitude of the fluctuations in the concentration of gene product. Top panel, activation and inhibition rate constants 0.05/t; bottom panel, activation and inhibition rate constants 0.075/t. (more...)

Nearly steady concentrations of P can be achieved either with very rapid alternation between activation and inactivation, or with extremely slow alternation (so that genes are either on or off most of the time). The mean concentration is determined by all 4 parameters as follows:

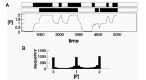
[P]_mean = (G_1act+G_2act)*k_act*k₃/(k_inact*k₄+k_act*k₄),       (6) where G_1act+G_2act = 2, and k_act and k_inact are the probabilities that a gene will be activated or inactivated, respectively, in a given time interval. If the values both k_act and k_inact decrease proportionally, or if the values of both k₃ and k₄ increase proportionally, the mean [P] is unchanged but the system spends an increasing fraction of time at [P]_min, or [P]_max, or 1/2[P]_max (Fig. 5A). The transition between high, medium, and low [P] is random and the probability that the system will be in one of these three states is distributed as shown in Figure 5B.

Figure 5

Very low rates of gene activation and inactivation result in product concentrations that dwell at zero, medium and high levels. A, top panel shows bars illustrating the on/off times of two alleles of a diploid above the resulting profile of gene product (more...)

Stabilizing Gene Expression

We are concerned with two patterns of stochastic gene expression. The first one is in the stochastic initiation of gene expression in a field where gene expression will eventually become homogeneous in all cells. The second is stochastic gene activation that leads to a salt-and-pepper pattern of two alternative stable states of gene expression in different cells (Fig. 2). In both cases it is necessary to turn a randomly fluctuating level of P into a stable state of gene expression that is spatially either homogeneous or heterogeneous. In the case of color patterns, the level of P must unambiguously specify one or another pigment synthesis pathway, so there must be a time point in development when the state of a gene becomes fixed.

One way of stabilizing initially stochastic expression is if the state of gene activation is “read” at a specific point in time, so that the state at that time (active or inactive) becomes fixed. A simple and possibly common way to do this is if [P] activates a process that makes further fluctuation in [P] irrelevant. P could, for instance, be a transcription factor that activates another gene with a more stable activation kinetics. Such a mechanism would require that the response to P behave as a threshold, so that P has no effect below the threshold concentration, and a full activating effect above the threshold. The value of the threshold would then determine the fraction of cells that express the phenotype specified by high levels of P. For instance, if the threshold is below the range of fluctuation of [P], all cells will express the phenotype, and if the threshold is above the range of fluctuation of [P], none will. A threshold within the range of variation in [P] will results in a random expression of alternative phenotypes in different cells. In this scenario, the mechanism that controls the threshold effectively controls the degree of stochasticity of the final pattern.

It is possible, however, to stabilize the expression level of P without the need to assume a threshold mechanism. One way to stabilize the activation of a gene is to reduce kinact to zero (or to a very small value relative to k_act) after a period of time. This could be achieved if the product P acts as an inhibitor of the inactivation reaction:

dG_act/dt = k_act* G_inact − k_inact*G_act/P,       (7)

so that as [P] rises, inactivation becomes progressively less probable. The mean [P] will approach [P]_max, but [P] will continue to fluctuate with a low amplitude (Fig. 6).

Figure 6

When the stochastic inactivation rate of a gene is much smaller than its stochastic activation rate, the gene product is stabilized and fluctuates with small amplitude at a high level. Here stabilization is achieved through inhibition of gene inactivation (more...)

Increasing the activation reaction relative to the inactivation reaction by means of a positive feedback from P

dG_act/dt = P* k_act* G_inact − k_inact*G_act,       (8) has a similar same effect (Fig. 7). Regulation of gene expression by the gene product (autocatalysis) is a common feature of the regulation of genetic regulatory mechanisms. This kind of feedback has one additional feature, in that it makes it possible to permanently inactivate expression of the gene.^3,7 Because gene activity is stochastic, the concentration of the gene product will fluctuate. If the feedback is not too strong then the concentration of the product can drop to zero, and this will effectively inactivate the gene because it brings the activation rate to zero (Equation 8 and Fig. 8). Of course, if the gene is initially inactive, this mechanism prevents it from being activated. Therefore a different stimulus that is not part of the feedback mechanism of P is required to activate gene expression. By itself, this mechanism only stabilizes the inactive state, not the active state, and [P] continues to fluctuate as long as the gene is not inactivated. The time required to become inactivated will have an exponential distribution.

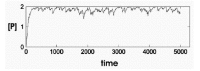
Figure 7

Stabilization of gene product level by positive feedback of gene product to gene activation rate.

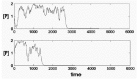
Figure 8

If positive feedback of gene product to gene activation rate is not strong fluctuations are large and can result in permanent inactivation of the gene.

The active state can be stabilized by feedback of P on the inactivation reaction, as suggested above, so a pseudo-bistable system (with [P] either zero or fluctuating at a high level) is

obtained by double feedback by P on both the activation and inactivation reactions giving (by combining equations 5, 7 and 8):

dG_1act/dt = P* k_act* G_1inact − k_inact*G_1act/P

dG_2act/dt = P* k_act* G_2inact − k_inact*G_2act/P       (9)

dP/dt = k₃*(G_1act + G_2act) − k₄*P

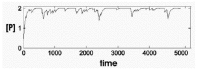
Figure 9 illustrates several sample traces of simulations with this set of equations for a diploid system. If an individual is heterozygous for G, so that G₁ is active and G₂ is not, maximum value of P is halved, and the probability that P will decline to zero in a given period of time greatly increased. An example of the distribution of times required for [P] to drop to zero in the diploid and haploid condition is shown in Figure 10. The means of these distributions, the percentage of cells with inactivated genes at a given time, and the exact difference between diploids and haploids, depends on the values of the parameters.

Figure 9

Double feedback results in a pseudo-bistable system in which gene product concentrations fluctuate with relatively low amplitude at a high level with occasional large excursions. When such a large excursion reduces the product concentration to zero the (more...)

Figure 10

Stochastic gene activation can result in haploinsufficiency. Frequency distribution of 1000 simulations of a haploid system with double feedback illustrating the times at which gene product drops to zero (cf Fig. 9), using the following parameter values: (more...)

Thresholds and Boundaries

During pattern formation in development, medium- and long-distance regulatory signals are often distributed in a smoothly graded fashion, and these graded signals eventually become translated into abrupt localized differences in gene expression. Mechanisms by which a graded signal can be translated into a discrete response have been extensively explored from a theoretical perspective. Most of the mechanisms studied so far establish thresholds or boundaries through some combination of cooperativity, lateral inhibition, bifurcation, and/or diffusive instability.^{8,9,10,11,12,13,14}

Cook et al (1998; ref. 3) studied the properties of a stochastic mechanism of gene activation in which an activator stimulated gene transcription with Michaelis-Menten kinetics. They assumed that the accumulation of the product above an arbitrary threshold level stimulated an all-or-none activation of a “phenotype.” They showed that this system exhibited a threshold-like response to graded input of the activator, with Hill coefficients ranging from 2.4 to 7.0. They showed that the steepness of the switch depended on the stability of gene activation: faster cycles of gene activation and inactivation produced sharper thresholds than relatively slower rates of gene activation and inactivation. These investigators were primarily interested in examining how the predictability of gene activation affected the response to a graded signal, and suggested that rapid cycling improved the response because it allowed a cell to sample stimulus intensity repeatedly before committing to a particular genetic response.

Here we are interested in the temporal and spatial distribution of the stochastic response. Instead of assuming an arbitrary threshold for the phenotype, we modeled a mechanism that stochastically inactivates the gene permanently or keeps it active with high probability. At a given time in development, the gene product is present or absent with a given probability that depends on the level of transcriptional activators and on the rates of product synthesis and decay.

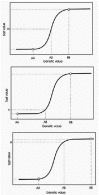
Spatial variation in parameter values will lead to spatial variation in the probability that the genes in a given cell will be activated or inactivated. Many transcription factors that regulate animal development are distributed as gradients. Smooth gradients of transcription factors are generally translated into more or less discrete spatial differences in the expression of regulated genes. In butterfly color patterns, transition between two colors is never abrupt but resembles a sigmoid transition (e.g., Fig. 11).

Figure 11

Boundaries between two color fields on the fore wing of Papilio glaucus, illustrating stochastic transitions. Colored scales in P. glaucus, as in most other butterflies, occur in parallel rows. Graphs show the frequency of light colored scales in each (more...)

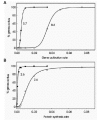
In our model, the activity of a transcription factor corresponds to the value kact, the rate constant for gene activation. A linear gradient of a transcription factor is simulated by a linear increase in the value of kact. The effect of such a gradient on stochastic gene activation in the absence of feedback regulation is shown in Figure 12A. The transition from zero to one hundred percent gene activation is sigmoid, with a large Hill coefficient that depends on the choice of parameter values. The response to a linear gradient, in the presence of feedback, is illustrated in Figure 13A. The transition is again sigmoid, with an even larger Hill coefficient. A linear gradient in the distribution of the activity of the enzyme that produces P also yields a sigmoid response in the distribution of gene product expression (Figs. 12B and 13B). The midpoint and steepness of the transition are determined by the shape of the gradient (linear or nonlinear) and the values of the parameters of the gene activation and expression mechanism (Fig. 14).

Figure 12

Response of the stochastic gene activation system described by equations (3) and (5) to a linear gradient of transcriptional activator activity (A), or a linear gradient in the activity of a product-synthesizing enzyme (B). Filled circles, all other parameters (more...)

Figure 13

Response of the stochastic gene activation system with double feedback regulation described by equations to a linear gradient of transcriptional activator activity (A), or a linear gradient in the activity of a product-synthesizing enzyme (B). Filled (more...)

Figure 14

Bivariate plots of the effect of variation in transcription factor activity and product synthesis activity on the level of P. Abscissa shows percentage of cells in which the genes were active at t = 10,000. In the upper flat regions [P]=[P]_max. In the (more...)

It is clear from these results that stochastic gene expression, with our without feedback regulation, produces threshold-like responses to graded input signals (see also ref. 3). Stochastic gene regulation is thus inherently a threshold mechanism. In butterfly wing patterns this is revealed by stochastic gradations at boundaries between regions of different colors (Fig. 11). Whether such stochastic transitions are a common feature of boundaries in other biological systems is not known. Experiments in which gene expression is visualized by in situ hybridization almost always reveal substantial stochastic expression at boundaries, so the involvement of stochastic processes in the regulation of thresholds and boundaries may be widespread.

Spatially Homogeneous Stochasticity

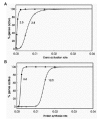
Butterflies are evidently able to regulate the stochastic pattern of gene expression in their color pattern with considerable accuracy. In sparse stochastic patterns, like those shown in Figure 3, the density gradients of colored scales are consistent from individual to individual, so these species are evidently able to control a precise proportionality of scales that are either on or off over large regions of their wing. It seems unlikely that these are cases in which the system is poised precisely on a steep transition with a high Hill coefficient, because such a situation would be extremely sensitive to individual variation. It is more likely that these kinds of individually invariant stable stochastic patterns exist in a region of geno-space where the Hill coefficients are rather small, such as the region in the foreground of Figure 14.

Thus in butterfly color patterns we see the entire range of stochastic expression, from alternative stability, to more or less sharp transition zones, to broadly distributed spatially homogeneous stochasticity. It is unlikely that each of these instances comes about through a totally different mechanism. Rather, it is more parsimonious to assume these are all variants of a common mechanism and that natural selection can produce genotypes that occur almost anywhere in the geno-space shown in Figure 14. An interesting possibility raised by this observation on butterflies is that tissues that are homogeneous for one gene activity may be spatially stochastic for another. Whether apparently homogeneous tissues are in fact mosaics of stochastic gene expression is an open question.

Dominance

Dominance is an emergent property of the mechanism by which a gene affects the value of a trait. In stochastic gene expression there is a sigmoidal relationship between genetic value and phenotypic value (Figs. 13 and 14). This nonlinearity leads to an interesting pattern of dominance among alleles. As shown in Figure 15, alleles that are on either extreme of a sigmoid distribution will be dominant over alleles that are on the transition. Alleles that are on the lower and upper flat regions of the distribution will be codominant only if they are perfectly symmetrical relative to the transition. If they are not, then the allele most distant from the transition will be dominant over the one closer to the transition, and this is independent of whether the allele is hypermorphic or hypomorphic.

Figure 15

A sigmoid relationship between genotype and phenotype has interesting consequences for the dominance relationships among alleles with different genetic values. In all three panels, open circles indicate the values of two homozygous genotypes. The alleles (more...)

Haploinsufficiency in the presence of a null-allele occurs if the remaining ‘active’ allele has a value that is less than twice the value of the transition midpoint. As can be seen in Figure 14, the value of this midpoint depends on the other genes in the system, so haploinsufficiency is a property of the entire genotype.

Evolution of dominance can occur either by mutational changes in the target gene or by changes in the genetic background.¹⁵ Mutational changes can be represented by the generation of new allelic values along the curve that describes the relationship between genotype and phenotype (e.g., Fig. 15). Changes in the genetic background, by contrast, change the shape of the genotype-phenotype curved, in effect changing the slope and inflection point of the sigmoid (for instance the shapes of the curves parallel to the x-axis depend on their position along the y axis in Fig. 14; here the gene represented by the y axis provides the genetic background for the gene represented by the x axis, and vice versa).

Alleles that are located the high or low plateaus of Figure 15 are not under selection, because their variation does not contribute to phenotypic variation. It is unlikely, therefore, that selection on alleles of the focal gene will contribute significantly to the evolution of dominance of that gene, particularly in regions where the transition between the low and high plateaus is very sharp. It is thus more likely that evolution of dominance in systems that are governed by stochastic gene expression occurs by evolution of the genetic background.

References

1.

McAdams HH, Arkin A. Stochastic mechanisms in gene expression. Proc Natl Acad Sci USA. 1997;94:814–819. [PMC free article: PMC19596] [PubMed: 9023339]

2.

Elowitz MB, Levine AJ, Siggia ED. et al. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. [PubMed: 12183631]

3.

Cook DL, Gerber AN, Tapscott SJ. Modeling stochastic gene expression: Implications for haploinsufficiency. Proc Natl Acad Sci USA. 1998;95:15641–15646. [PMC free article: PMC28097] [PubMed: 9861023]

4.

Brunetti C, Paddock S, Carroll S. The generation and diversification of butterfly eyespot color patterns. Curr Biol. 2001;11:1578–1585. [PubMed: 11676917]

5.

Ko MSH. Induction mechanisms of a single gene molecule: Stochastic or deterministic? BioEssays. 1992;14:341–346. [PubMed: 1637366]

6.

Ko MSH. A stochastic model for gene induction. J Theoret Biol. 1991;153:181–194. [PubMed: 1787735]

7.

Kepler TB, Elston TC. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys J. 2001;81:3116–3136. [PMC free article: PMC1301773] [PubMed: 11720979]

8.

Turing AM. The chemical basis of morphogenesis. Ser B, London: Phil Trans Roy Soc. 1952;237:37–72.

9.

Lewis J, Slack JMW, Wolpert L. Thresholds in development. J Theor Biol. 1977;65:579–590. [PubMed: 859349]

10.

Meinhardt H. Models of Biological Pattern FormationLondon: Academic Press,1982 .

11.

Meinhardt H. Models for positional signaling with applications to the dorsoventral patterning of insects and segregation into different cell types. Development. 1989;(Suppl):169–180. [PubMed: 2699854]

12.

Meinhardt H. Organizers and axes formation as a self-organizing process. Int J Dev Biol. 2001;45:177–188. [PubMed: 11291845]

13.

Oster GF. Lateral inhibition models of developmental processes. Math Biosci. 1988;90:265–286.

14.

Murray JD. Mathematical BiologyNew York: Springer-Verlag,1989 .

15.

Gilchrist MA, Nijhout HF. Nonlinear developmental processes as sources of dominance. Genetics. 2001;159:423–432. [PMC free article: PMC1461774] [PubMed: 11560916]