NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
National Clinical Guideline Centre (UK). Blood Transfusion. London: National Institute for Health and Care Excellence (NICE); 2015 Nov. (NICE Guideline, No. 24.)
L.1. Introduction
The results of conventional meta-analyses of direct evidence alone (as presented in the GRADE profiles in chapter 6 and forest plots in appendix K.2) does not help inform which intervention is most effective as an alternative to blood transfusion in surgical patients. The challenge of interpretation has arisen for two reasons:
- In isolation, each pair-wise comparison does not inform the choice among the different treatments; in addition direct evidence is not available for some pair-wise comparisons in a randomised controlled trial (for example, ICS vs. PCS).
- There are frequently multiple overlapping comparisons (for example, ICS+TXA vs. TXA, ICS+PCS+TXA vs. TXA and ICS+PCS+TXA vs. ICS+PCS), that could potentially give inconsistent estimates of effect.
To overcome these problems, a hierarchical Bayesian network meta-analysis (NMA) was performed. This type of analysis allows for the synthesis of data from direct and indirect comparisons without breaking randomisation and allows for the ranking of different interventions. In this case, in order of efficacy, the outcomes were defined as:
- the number of people who are transfused with allogeneic blood
- the units of allogeneic blood transfused
- length of stay in hospital
The analysis also provided estimates of effect (with 95% credible intervals) for each intervention compared to one another and compared to a single baseline risk (in this case the baseline treatment was standard treatment). These estimates provide a useful clinical summary of the results and facilitate the formation of recommendations based on the best available evidence. Furthermore, these estimates were used to parameterise treatment effectiveness in the de novo cost-effectiveness modelling presented in appendix M.
Conventional fixed effects meta-analysis assumes that the relative effect of one treatment compared to another is the same across an entire set of trials. In a random effects model, it is assumed that the relative effects are different in each trial but that they are from a single common distribution and that this distribution is common across all sets of trials.
Network meta-analysis requires an additional assumption over conventional meta-analysis. The additional assumption is that intervention A has the same effect on people in trials of intervention A compared to intervention B as it does for people in trials of intervention A versus intervention C, and so on. Thus, in a random effects network meta-analysis, the assumption is that intervention A has the same effect distribution across trials of A versus B, A versus C and so on.
This specific method is usually referred to as mixed-treatment comparisons analysis but the term network meta-analysis will be used to refer generically to this kind of analysis. It was agreed that this would be best since the term “network” better describes the data structure, whereas “mixed treatments” could easily be misinterpreted as referring to combinations of treatments.
L.2. Methods
L.2.1. Study selection and data collection
To estimate the relative risks, an NMA was performed that simultaneously used all the relevant RCT evidence from the clinical evidence review. As with conventional meta-analyses, this type of analysis does not break the randomisation of the evidence, nor does it make any assumptions about adding the effects of different interventions. The effectiveness of a particular treatment strategy combination will be derived only from randomised controlled trials that had that particular combination in a trial arm.
From the outset, efforts were made to minimise any clinical or methodological heterogeneity by focusing the analysis on RCTs with comparable routes of administration of treatments, identifying equivalent outcomes and including only RCTs on cell salvage that were conducted after 2003 as this was defining watershed in transfusion practice (also see rationale in section 6.2.3, chapter 6). All of the dosages of drugs in the included RCTs were within the therapeutic range as indicated by the BNF. In consultation with the GDG, it was agreed that an NMA would be performed for alternatives to blood transfusion including combinations of different types of cell salvage and/or tranexamic acid. The evidence on these interventions included multiple comparisons and an NMA would allow the synthesis of the evidence in a more comprehensive way.
As such, five networks of evidence were identified, defined by outcome measure. Three networks were in the high risk group and two were in the moderate risk group (For definitions of risk groups see section 6, Chapter 6.4.2). The networks were as follows:
High risk group
- Network 1: Number of people receiving allogeneic transfusions
- Network 2: Units of allogeneic blood transfused
- Network 3: Length of stay in hospital
Moderate risk group
- Network 4: Number of people receiving allogeneic transfusions
- Network 5: Units of allogeneic blood transfused
L.2.2. Outcome measures
The NMA evidence reviews for interventions considered three clinical efficacy outcomes identified from the clinical evidence review; number of people receiving allogeneic transfusions, units of allogeneic blood transfused and length of stay in hospital. Other outcomes were not considered for the NMA as they were infrequently reported across the studies. The GDG considered the number of people receiving allogeneic transfusions and units of allogeneic blood transfused to be the most important clinical outcomes for testing effectiveness of alternatives to reduce blood transfusion requirements.
L.2.3. Comparability of interventions
The interventions compared in the model were those found in the randomised controlled trials and included in the clinical evidence review already presented in chapter 6 of the full guideline. If an intervention was evaluated in a study that met the inclusion criteria for the network (that is if it reported at least one of the outcomes of interest and matched the inclusion criteria for the meta-analysis) then it was included in the network meta-analysis, otherwise it was excluded.
The treatments included in each network are shown in Table 1.
Table 1
Treatments included in network meta-analysis.
The details of these interventions can be found in the clinical evidence review in chapter 6 of the full guideline and evidence tables in section H.2, appendix H.
L.2.4. Baseline risk
The baseline risk is defined here as the risk of achieving the outcome of interest in the standard treatment group. This figure is useful because it allows the conversion of the results of the NMA from odds ratios to relative risks.
Baseline odds were derived by the logistic regression in WinBUGS. This approach has the advantage that baseline and relative effects are both modelled on the same log odds scale, and also ensures that the uncertainty in the estimation of baseline and relative effects is accounted for in the model. This method produced baseline odds [mean (SD)] as follows:
- -0.06809 (1.188) for number of patients receiving allogeneic transfusions in the high risk group
- -0.5185 (1.444) for number of patients receiving allogeneic transfusions in the moderate risk group
A baseline risk model of mortality was conducted in both risk groups to estimate baseline mortality for the economic model. The method produced baseline relative risk [mean (SD)] of 0.0343 (0.01135) in the high risk group. In the moderate risk group, this was 0.00162 (0.002384). For details of data informing these models, please refer to the full cost- effectiveness analysis (section M.2.3.3, Appendix M).
L.2.5. Statistical analysis
A hierarchical Bayesian network meta-analysis (NMA) was performed using the software WinBUGS. We adapted a three-arm random effects model template for the networks, from the University of Bristol website (https://www.bris.ac.uk/cobm/research/mpes/mtc.html). This model accounts for the correlation between study level effects induced by multi-arm trials.
In order to be included in the analysis, a fundamental requirement is that each treatment is connected directly or indirectly to every other intervention in the network. For each outcome subgroup, a diagram of the evidence network is presented in section L.3.
The model used was a random effects logistic regression model, with parameters estimated by Markov chain Monte Carlo simulation. As it was a Bayesian analysis, for each parameter the evidence distribution is weighted by a distribution of prior beliefs. These were estimated from the baseline models for the dichotomous outcomes using the following equations.
- Predictive probability of response (MeanA) =mean of mu.new
- Precision (PrecA)=1/(standard deviation of mu.new)2
A non-informative prior distribution was used to maximise the weighting given to the data for continuous outcomes. These priors were normally distributed with a mean of 0 and standard deviation of 10,000.
For the analyses, a series of 100,000 burn-in simulations were run to allow convergence and then a further 100,000 simulations were run to produce the outputs. For the baseline analyses, a series of 50,000 burn-in simulations were run to allow convergence and then a further 50,000 simulations were run to produce the outputs. Convergence was assessed by examining the history and kernel density plots.
The goodness of fit of the model was tested by calculating the residual deviance. If the residual deviance is close to the number of unconstrained data points (the number of trial arms in the analysis) then the model is explaining the data well.
The results, in terms of relative risk, of pair-wise meta-analyses are presented in the clinical evidence review (Chapter 6).
The aim of the NMA was to calculate treatment specific log odds ratios and relative risks for response to be consistent with the comparative effectiveness results presented elsewhere in the clinical evidence review and for ease of interpretation. Let BO, , and p denote the baseline odds, treatment specific odds, treatment specific log odds ratio and absolute probability respectively. Then:
And:
Once the treatment specific probabilities for response were calculated, these were divided by the baseline probability (pb) to get treatment specific relative risks (rrb):
This approach has the advantage that baseline and relative effects are both modelled on the same log odds scale, and also ensures that the uncertainty in the estimation of both baseline and relative effects is accounted for in the model.
The overall ranking of interventions according to their relative risk compared to control group and counting the proportion of simulations of the Markov chain in which each intervention had the highest relative risk.
Due to the skewness of the data, the NMA relative risks and rank results are reported as medians rather than means (as in the direct comparisons) to give a more accurate representation of the ‘most likely’ value.
A key assumption behind NMA is that the network is consistent. In other words, it is assumed that the direct and indirect treatment effect estimates do not disagree with one another. Discrepancies between direct and indirect estimates of effect may result from several possible causes. First, there is chance and if this is the case then the network meta-analysis results are likely to be more precise as they pool together more data than conventional meta-analysis estimates alone. Second, there could be differences between the trials included in terms of their clinical or methodological characteristics. Differences that could lead to inconsistency include:
- Different populations
- Different interventions
- Different routes of administration
This heterogeneity is a problem for network meta-analysis but may be dealt with by subgroup analysis, meta-regression or by carefully defining inclusion criteria. In this analysis, sub-group analyses based on various factors such as haemoglobin status at baseline, different haemoglobin thresholds for blood transfusion and different routes of administration was undertaken to account for heterogeneity in the pair wise meta-analyses. Inconsistency in the network, caused by heterogeneity, was assessed subjectively by comparing the odds ratios for binary outcomes and mean differences for continuous outcomes from the direct evidence (from pair-wise meta-analysis) with the corresponding effects estimated from the combined direct and indirect evidence (from NMA). We assumed the evidence to be inconsistent where the odds ratio or mean difference from the NMA did not fit within the confidence interval of the odds ratio or mean difference from the direct comparison. We further tested for inconsistency by developing inconsistency models for networks of binary outcomes (number of patients transfused). We assumed the evidence to be consistent when the difference in deviance information criterion (DiC) values between the consistency and the inconsistency models was less then 3-5. No inconsistency was identified.
L.3. Results
A total of 129 studies from the original evidence review met the inclusion criteria for at least one network. Figure 176 – Figure 180 show the four networks created by eligible comparisons for each NMA. The number on the line linking two treatments indicates the number of studies included that assessed that direct comparison.
L.3.1. NMA models
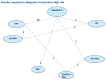
Figure 176
Adults-High risk group: Network for number of patients receiving allogeneic transfusions.

Figure 177
Adults-High risk group: Network for units of allogeneic blood transfused.

Figure 178
Adults-High risk group: Length of stay in hospital.
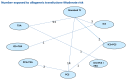
Figure 179
Adults-Moderate risk group: Network for number of patients receiving allogeneic transfusions.

Figure 180
Adults-Moderate risk group: Network for units of allogeneic blood transfused.
L.3.2. Trial data
L.3.2.1. High risk group
Trial data from the 56 studies included in the NMA for number of adult patients receiving allogeneic transfusions are shown in Table 2. The trial data from the 23 studies included in the NMA for number of units of allogeneic blood transfused are shown in Table 3. The trial data from the 10 studies included in the NMA for length of stay in hospital are shown in Table 4.
Table 2
Study data for number of patients receiving allogeneic transfusions.
Table 3
Study data for units of allogeneic blood transfused.
Table 4
Study data for length of stay.
L.3.2.2. Moderate risk group
The trial data from the 73 studies included in the NMA for number of patients receiving allogeneic transfusions are shown in Table 5. The trial data from the 16 studies included in the NMA for number of units of allogeneic transfusions received are shown in Table 6.
Table 5
Study data for number of patients receiving allogeneic transfusions.
Table 6
Study data for units of allogeneic blood transfused.
L.3.3. Network 1: Number of patients receiving allogeneic transfusions (Adults-high risk group)
Table 7 summarises the results of the conventional meta-analyses in terms of odds ratios generated from studies directly comparing different interventions, together with the results of the NMA in terms of odds ratios for every possible treatment comparison.
Table 7
Odds ratios for number of patients receiving allogeneic transfusions (Adults- high risk group).
Figure 181 shows the rank of each intervention compared to the others. Figure 182 shows the median relative risk of each intervention compared to the others. The rank is based on the relative risk compared to baseline and indicates the probability of being the best treatment, second best, third best and so on among the 7 different interventions being evaluated.

Figure 181
Rank order for treatments based on number of patients receiving allogeneic transfusions.

Figure 182
Relative risk (median) for number of patients receiving allogeneic transfusions.
Based on the relative risks from the direct comparisons, efficacy as assessed by number of patients receiving allogeneic transfusions favours tranexamic acid, post-operative cell salvage, intra-operative cell salvage and the combination of intra-operative and post-operative cell salvage over standard treatment and the combination of intra-operative cell salvage and tranexamic acid over intra-operative cell salvage. No other treatment effects reached statistical significance.
The random effects model used for the NMA is a relatively good fit, with a residual deviance of 125.8 reported. This corresponds fairly well to the total number of trial arms, 112. The between study variance was 0.2149 (0.01189, 0.4721). No inconsistency was identified between the direct and NMA results for any comparison. All the median odds ratios from the NMA lie within the 95% confidence interval from the direct comparison of the same comparisons (see Table 42). The DiC value from the network was 624.777 and the DiC value from the inconsistency model was 626.856.
Evidence statement
A network meta-analysis of 56 studies comparing seven treatments suggested that PCS is ranked as the best treatment, ICS+TXA is ranked second, TXA, ICS+PCS+TXA and ICS+PCS are jointly ranked fourth and standard treatment ranked least effective at reducing the number of adult patients receiving allogeneic transfusions in the high risk group, but there was considerable uncertainty.
L.3.4. Network 2: Units of allogeneic blood transfused (Adults- high risk group)
Table 8 summarises the results of the conventional meta-analyses in terms of mean differences generated from studies directly comparing different interventions, together with the results of the NMA in terms of mean differences for every possible treatment comparison.
Table 8
Mean differences for units of allogeneic blood transfused (Adults- high risk group).
Figure 183 shows the rank of each intervention compared to the others. Figure 184 shows the median of the mean differences of each intervention compared to the others. The rank is based on the mean difference compared to baseline and indicates the probability of being the best treatment, second best, third best and so on among the 5 interventions being evaluated.
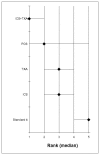
Figure 183
Rank order for treatments based on units of allogeneic blood transfused.

Figure 184
Mean differences (median) for units of allogeneic blood transfused.
Based on the direct comparisons (first results column Table 8), efficacy as assessed by reduced number of units of allogeneic transfusions received favours intra-operative cell salvage, post-operative cell salvage, tranexamic acid over standard treatment, and the combination of intra-operative cell salvage and tranexamic acid over intra-operative cell salvage. No other treatment effects reached statistical significance.
The random effects model used for the NMA is a relatively good fit, with a residual deviance of 54.55 reported. This corresponds fairly well to the total number of trial arms, 46. The between study variance was 0.5521 (0.2752, 1.078). The DiC value for the network was 61.454. No inconsistency was identified between the direct and NMA results for any comparison. All the mean differences from the NMA lie within the 95% confidence interval from the direct comparison of the same comparisons.
Evidence statement
A network meta-analysis of 23 studies comparing five treatments suggested that ICS+TXA is ranked as the best treatment, PCS is ranked second, TXA and ICS are jointly ranked third, and standard treatment ranked least effective at reducing the number of units of allogeneic blood transfusions in adult patients in the high risk group, but there was considerable uncertainty.
L.3.5. Network 3: Length of stay in hospital (Adults- high risk group)
Table 9 summarises the results of the conventional meta-analyses in terms of mean differences generated from studies directly comparing different interventions, together with the results of the NMA in terms of mean differences for every possible treatment comparison.
Table 9
Mean differences for length of stay in hospital (Adults- high risk group).
Figure 185 shows the rank of each intervention compared to the others. Figure 186 shows the median of the mean differences of each intervention compared to the others. The rank is based on the mean difference compared to baseline and indicates the probability of being the best treatment, second best, third best and so on among the 6 different interventions being evaluated.
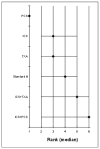
Figure 185
Rank order for treatments based on length of stay in hospital.
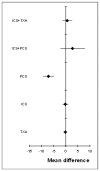
Figure 186
Mean differences (median) for length of stay in hospital.
Based on the direct comparisons (first results column Table 9), efficacy as assessed by reduced length of stay in hospital favours post-operative cell salvage over standard treatment. No other treatment effects reached statistical significance.
The random effects model used for the NMA is a relatively good fit, with a residual deviance of 16.82 reported. This corresponds fairly well to the total number of trial arms, 20. The between study variance was 0.261 (0.01098, 1.459). The DiC value for this network was 44.320. No inconsistency was identified between the direct and NMA results for any comparison. All the mean differences from the NMA lie within the 95% confidence interval from the direct comparison of the same comparisons.
Evidence statement
A network meta-analysis of 10 studies comparing six treatments suggested that PCS is ranked as the best treatment, ICs and TXA are jointly ranked third, standard treatment is ranked fourth, ICS+TXA is ranked fifth and ICS+PCS is ranked least effective at reducing length of stay in hospital in adult patients in the high risk group, but there was considerable uncertainty.
L.3.6. Network 4: Number of patients receiving allogeneic blood (Adults- moderate risk group)
Table 10 summarises the results of the conventional meta-analyses in terms of risk ratios generated from studies directly comparing different interventions, together with the results of the NMA in terms of risk ratios for every possible treatment comparison.
Table 10
Risk ratios for number of patients receiving allogeneic transfusions (Adults-moderate risk group).
Figure 187 shows the rank of each intervention compared to the others. Figure 188 shows the median relative risk of each intervention compared to the others. The rank is based on the relative risk compared to baseline and indicates the probability of being the best treatment, second best, third best and so on among the 8 different interventions being evaluated.

Figure 187
Rank order for treatments based on number of patients receiving allogeneic transfusions.
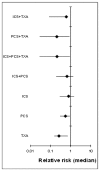
Figure 188
Relative risk (median) for number of patients receiving allogeneic transfusions.
Based on the direct comparisons (first results column Table 10), efficacy as assessed by number of patients receiving allogeneic transfusions favours the use of post-operative cell salvage or tranexamic acid over standard treatment. No other treatment effects reached statistical significance.
The random effects model used for the NMA is a relatively good fit, with a residual deviance of 145.2 reported. This corresponds fairly well to the total number of trial arms, 147. The between study variance was 0.7827 (0.5682, 1.057). On evaluating inconsistency by comparing the odds ratios, the NMA estimated odds ratio for ICS+PCS vs. standard treatment (0.4954 [0.1385, 1.713]) lay outside of the confidence interval of the odds ratio estimated from the direct comparison (0.83[0.51, 1.35]). However, the DiC values generated from the network and the inconsistency models were similar highlighting that there was no inconsistency. The DiC value from the network was 745. 119 and the DiC value from the inconsistency model was 745.202.
Evidence statement
A network meta-analysis of 73 studies comparing eight treatments suggested that PCS+TXA is ranked as the best treatment, ICS +TXA is ranked second, TXA is ranked fourth, ICS+TXA, ICS+PCS and PCS are jointly ranked fifth, ICS is ranked sixth and standard treatment is ranked least effective at reducing the number of adult patients receiving allogeneic transfusions in the moderate risk group, but there was considerable uncertainty.
L.3.7. Network 5: Units of allogeneic blood transfused (Adults- moderate risk group)
Table 11 summarises the results of the conventional meta-analyses in terms of mean differences generated from studies directly comparing different interventions, together with the results of the NMA in terms of mean differences for every possible treatment comparison.
Table 11
Mean differences for units of allogeneic blood transfused (Adults- Moderate risk group).
Figure 189 shows the rank of each intervention compared to the others. Figure 190 shows the median of the mean differences of each intervention compared to the others. The rank is based on the mean difference compared to baseline and indicates the probability of being the best treatment, second best, third best and so on among the 4 interventions being evaluated.

Figure 189
Rank order for treatments based on units of allogeneic blood transfused.
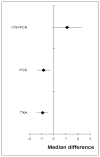
Figure 190
Mean differences (median) for units of allogeneic blood transfused.
Based on the direct comparisons (first results column Table 11), efficacy as assessed by reduced number of units of allogeneic transfusions received favours tranexamic acid and post-operative cell salvage over standard treatment, and standard treatment over the combination of intra-operative cell salvage and post-operative cell salvage. No other treatment effects reached statistical significance.
The random effects model used for the NMA is a relatively good fit, with a residual deviance of 33.45 reported. This corresponds fairly well to the total number of trial arms, 33. The DiC value of the network was 8.237. No inconsistency was identified between the direct and NMA results for any comparison. All the mean differences from the NMA lie within the 95% confidence interval from the direct comparison of the same comparisons.
Evidence statement
A network meta-analysis of 16 studies comparing four treatments suggested that PCS and TXA are jointly ranked as the best treatment, standard treatment is ranked third and the combination of ICS+PCS is ranked least effective at reducing the number of units of allogeneic blood transfusions in adult patients in the moderate risk group, but there was some uncertainty.
L.4. Discussion
Based on the results of conventional meta-analyses of direct evidence, as has been previously presented in chapter 6 and appendix 6.5.2, deciding upon the most effective intervention as an alternative to blood transfusion in surgical patients is challenging. In order to overcome the difficulty of interpreting the conclusions from numerous separate comparisons, network meta-analysis of the direct evidence were performed.
Our analyses were divided into two risk groups- high and moderate risk groups (For details of stratification, please refer section 6.2.2, chapter 6). 73 studies formed 3 networks, each for a different outcome, in the high risk group; 56 studies were included in a network for one outcome in the moderate risk group. Four treatment interventions were evaluated alone or in combination with one another in these analyses.
The findings from the NMA were used to facilitate the GDG in decision making when developing recommendations for alternatives to blood transfusion in surgical patients.
In the first network of number of adult patients receiving allogeneic transfusions in the high risk group, all treatments were found to be superior to standard treatment; ICS+TXA was found to be superior to TXA, ICS, ICS+PCS+TXA, ICS+PCS; TXA alone was found to be superior to ICS, ICS+PCS+TXA, ICS+PCS; ICS+PCS+TXA was found to be superior to ICS, ICS+PCS; ICS+PCS was found to be superior to ICS alone.
In the ranking of treatments PCS was ranked as the best treatment although there is considerable uncertainty about this estimate as the credible intervals are quite wide; the GDG also discussed concerns regarding the applicability of this evidence and highlighted that it may not be an appropriate intervention in all high risk surgeries (for details, please refer the full cost-effectiveness analysis in Appendix M and the LETR). ICS+TXA was ranked second and the GDG noted that in surgical patients who were expected to have very high blood loss, this may well be the most appropriate blood saving intervention. TXA was ranked third, with much smaller credible intervals only spanning three ranking positions.
In the second network of number of units of allogeneic transfusions received in the high risk group, all treatments were found to be superior to standard treatment; ICS+TXA was found to be superior to PCS, TXA, ICS; PCS was found to be superior to TXA,ICS; TXA and ICS were found to be superior to standard treatment.
In the ranking of treatments ICS +TXA was ranked as the best treatment with very precise credible intervals spanning only two ranking interventions; the GDG agreed that ICS+TXA was the most blood saving intervention in the high risk group in terms of number of units transfused. PCS was ranked second ICS+TXA was ranked second, but with very wide credible intervals; TXA and ICs were jointly ranked third.
In the third network of length of stay in hospital in the high risk group, all treatments were found to be superior to ICS+PCS; PCS was found to be superior to ICS, TXA, Standard treatment, ICS+TXA; ICS was found to be superior to TXA, Standard treatment, ICS+TXA; Standard treatment was found to be superior to ICS+TXA.
In the ranking of treatments PCS was ranked as the best treatment with very precise credible intervals. However, the GDG noted that this was based on data from one study where the baseline group had a very high length of stay. ICS and TXA were jointly ranked as the second best interventions having reduced length of stay, with identical credible intervals. Standard treatment was ranked as the third best intervention over ICS+TXA and ICS+PCS, but all three had very wide credible intervals spanning greater than three ranking interventions.
In the fourth network of number of adult patients receiving allogeneic transfusions in the moderate risk group, all treatments were found to be superior to standard treatment; PCS+TXA was found to be superior to ICS+PCS+TXA, TXA, ICS+TXA, ICS+PCS, PCS, ICS; ICS+PCS+TXA was found to be superior to TXA, ICS+TXA, ICS+PCS, PCS; TXA alone was found to be superior to ICS+TXA, ICS+PCS, PCS, ICS; ICS+TXA was found to be superior to ICS+PCS, PCS, ICS; ICS+PCS was found to be superior to PCS, ICS; PCS was found to be superior to ICS.
In the ranking of treatments PCS+TXA was ranked first and ICS+PCS+TXA was ranked second, although both rankings had very wide credible intervals spanning greater than five treatment ranking interventions. TXA was ranked third, but with much smaller credible intervals only spanning three ranking positions. ICS +TXA and ICS+PCS were jointly ranked fifth with very wide credible intervals spanning greater than six treatment ranking interventions. PCS was also ranked fifth, but had smaller credible intervals spanning four treatment ranking interventions. ICs was ranked sixth but again, had very wide credible intervals.
All four networks seem to fit well, as demonstrated by residual deviance and no inconsistencies in the networks were found.
In summary, the three outcomes chosen for this analysis were considered to be among the most important for assessing efficacy of alternatives to blood transfusion in adult surgical patients in the high and moderate risk groups. All of these outcomes contributed to the cost effectiveness analysis (see Appendix M).
L.5. Conclusion
This analysis allowed us to combine findings from many different comparisons presented in the reviews for alternatives to blood transfusion even when direct comparative data was lacking.
Overall, the GDG agreed that results of the four networks in the high and moderate risk groups were not conclusive. It was acknowledged that the combination of intra-operative cell salvage and tranexamic acid and, tranexamic acid alone were likely to be the most effective blood saving interventions and therefore appropriate as alternatives to blood transfusion in adult surgical patients.
It should be noted that this analysis does not take into account the adverse effect profile of these treatments, but known profiles have been taken into account in the development of the associated recommendations. For details of the rationale and discussion around the discussion leading to recommendations, please refer the section linking the evidence to the recommendations (section 4.5, chapter 4).
L.6. WinBUGS codes
L.6.1. WinBUGS code for assessment of baseline risk of receiving allogeneic transfusions (High risk group)
# Baseline random effects model
model{ # *** PROGRAM STARTS
for (i in 1:ns){ # LOOP THROUGH STUDIES
r[i] ∼ dbin(p[i],n[i]) # Likelihood
logit(p[i]) <- mu[i] # Log-odds of response
mu[i] ∼ dnorm(m,tau.m) # Random effects model
}
mu.new ∼ dnorm(m,tau.m) # predictive dist. (log-odds)
m ∼ dnorm(0,.0001) # vague prior for mean
var.m <- 1/tau.m # between-trial variance
tau.m <- pow(sd.m,-2) # between-trial precision = (1/between-trial variance)
sd.m ∼ dunif(0,5) # vague prior for between-trial SD
#tau.m ∼ dgamma(0.001,0.001)
#sd.m <- sqrt(var.m)
logit(R) <- m # posterior probability of response
logit(R.new) <- mu.new # predictive probability of response
}
Data
list(ns=48) # ns=number of studies
r[] n[]
31 41
7 31
21 29
8 25
1 33
30 30
3 24
19 49
64 102
10 15
27 38
5 17
51 96
10 43
23 50
7 25
41 165
12 20
8 33
21 40
8 39
12 31
221 278
54 59
27 50
6 30
54 115
8 40
17 108
63 140
9 14
4 20
8 14
12 20
37 40
4 20
13 19
27 44
16 44
10 31
27 106
9 14
18 24
11 15
43 75
22 50
74 100
108 177
END
Inits
list(mu=c( 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0,
0,0,0,0,0,0,0,0), sd.m=1, m=0)
list(mu = c(1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1,
-1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1,-1,-1,-1), sd.m=2, m= -1)
list(mu = c(1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1,
1,1,1,1,1,1,1,1), sd.m = 0.5, m = 1)
L.6.2. WinBUGS code for number of adult patients receiving allogeneic transfusions (High risk group)
NUMBER TRANSFUSED HIGH RISK
# Binomial likelihood, logit link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ∼ dbin(p[i,k],n[i,k]) # binomial likelihood
logit(p[i,k]) <- mu[i] + delta[i,k] # model for linear predictor
rhat[i,k] <- p[i,k] * n[i,k] # expected value of the numerators
#Deviance contribution
dev[i,k] <- 2 * (r[i,k] * (log(r[i,k])-log(rhat[i,k]))
+ (n[i,k]-r[i,k]) * (log(n[i,k]-r[i,k]) - log(n[i,k]-rhat[i,k]))) }
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(md[i,k],taud[i,k])
# mean of LOR distributions (with multi-arm trial correction)
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k]
# precision of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k
# adjustment for multi-arm RCTs
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]])
# cumulative adjustment for multi-arm trials
sw[i,k] <- sum(w[i,1:k-1])/(k-1)
}
}
totresdev <- sum(resdev[]) # Total Residual Deviance
d[1]<-0 # treatment effect is zero for reference treatment
# vague priors for treatment effects
for (k in 2:nt){ d[k] ∼ dnorm(0,.0001) }
sd ∼ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# Provide estimates of treatment effects T[k] on the natural (probability) scale
# Given a Mean Effect, meanA, for 'standard' treatment A,
# with precision (1/variance) precA
A ∼ dnorm(meanA,precA)
for (k in 1:nt) { logit(T[k]) <- A + d[k] }
rr [1] < -1
for (k in 2:nt) {rr[k]<-T[k]/T[1] }
for (c in 1:(nt-1))
{ for (k in (c+1):nt)
{ lor[c,k] <- d[k] - d[c]
log(or[c,k]) <- lor[c,k]
lrr[c,k] <- log(rr[k]) - log(rr[c])
log(rrisk[c,k]) <- lrr[c,k] }}
for (k in 1:nt) {
rk[k]<-rank(rr[],k)
best[k]<-equals(rank(rr[],k),1)}
} # *** PROGRAM ENDS
Data
# ns= number of studies; nt=number of treatments
list(ns=56, nt=7, meanA=-0.07213, precA=0.708544479588251)
r[,1] r[,2] n[,1] n[,2] t[,1] t[,2] na[]
31 21 41 40 1 4 2
7 4 31 30 1 4 2
21 17 29 30 1 4 2
8 7 25 25 1 4 2
1 2 33 32 1 3 2
30 19 30 30 1 3 2
3 1 24 23 1 3 2
19 6 49 41 1 3 2
64 41 102 98 1 5 2
10 8 15 15 1 5 2
13 9 50 52 4 6 2
27 20 60 60 4 6 2
19 9 26 24 4 6 2
12 5 20 20 4 6 2
73 57 103 99 4 6 2
13 12 29 24 2 6 2
14 13 50 50 5 7 2
33 31 111 102 2 7 2
27 20 38 38 1 2 2
5 6 17 20 1 2 2
51 51 96 97 1 2 2
10 8 43 44 1 2 2
23 15 50 50 1 2 2
7 2 25 22 1 2 2
41 24 165 147 1 2 2
12 7 20 20 1 2 2
8 5 33 33 1 2 2
21 15 40 40 1 2 2
8 7 39 40 1 2 2
12 7 31 29 1 2 2
221 166 278 274 1 2 2
54 42 59 58 1 2 2
27 8 50 50 1 2 2
6 3 30 32 1 2 2
54 37 115 116 1 2 2
8 3 40 36 1 2 2
17 0 108 106 1 2 2
63 35 140 143 1 2 2
9 7 14 15 1 2 2
4 2 20 20 1 2 2
8 9 14 16 1 2 2
12 15 20 41 1 2 2
37 29 40 42 1 2 2
4 3 20 20 1 2 2
13 14 19 19 1 2 2
27 28 44 42 1 2 2
16 12 44 37 1 2 2
10 7 31 62 1 2 2
27 11 106 104 1 2 2
9 2 14 16 1 2 2
18 12 24 24 1 2 2
11 13 15 15 1 2 2
43 22 75 75 1 2 2
22 15 50 50 1 2 2
74 60 100 100 1 2 2
108 98 177 189 1 4 2
END
Initial Values
list(
d=c(NA,0,0,0,0,0,0),
sd=.2,
mu=c(2,0,3,0,2,-2,2,-2,-1,3,2,-2,1,3,1,1,2,-3,2,-2,-2,1,0,-3,3,0,-3,-2,-3,-2,3,-3,0,-1,-3,2,1,3,-
2,2,2,0,1,2,0,0,-2,1,-2,-2,-3,-2,1,2,1,2))
list(
d=c(NA,1,1,1,1,1,1),
sd=.1,
mu=c(2,1,3,1,2,0,2,0,-1,3,2,0,1,3,1,1,2,-3,2,0,0,1,1,-3,3,1,-3,0,-3,0,3,-3,1,-1,-
3,2,1,3,0,2,2,1,1,2,1,1,0,1,0,0,-3,0,1,2,1,2))
list(
d=c(NA,0.5,0.5,0.5,0.5,0.5,0.5),
sd=.15,
mu=c(2,0.5,3,0.5,2,-2,2,1,-1,3,2,1,1,3,1,1,2,-3,2,1,1,1,0.5,-3,3,0.5,-3,1,-3,1,3,-3,0.5,-1,-
3,2,1,3,1,2,2,0.5,1,2,0.5,0.5,1,1,1,1,-3,-2,1,2,1,2))
L.6.3. WinBUGS code for inconsistency model for number of adult patients receiving allogeneic transfusions (High risk group)
High risk number transfused
56 trials
7 treatments
# Binomial likelihood, logit link, inconsistency model
# Random effects model
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
delta[i,1]<-0 # treatment effect is zero in control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ∼ dbin(p[i,k],n[i,k]) # binomial likelihood
logit(p[i,k]) <- mu[i] + delta[i,k] # model for linear predictor
#Deviance contribution
rhat[i,k] <- p[i,k] * n[i,k] # expected value of the numerators
dev[i,k] <- 2 * (r[i,k] * (log(r[i,k])-log(rhat[i,k]))
+ (n[i,k]-r[i,k]) * (log(n[i,k]-r[i,k]) - log(n[i,k]-rhat[i,k])))
}
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(d[t[i,1],t[i,k]] ,tau)
}
}
totresdev <- sum(resdev[]) # Total Residual Deviance
for (c in 1:(nt-1)) { # priors for all mean treatment effects
for (k in (c+1):nt) { d[c,k] ∼ dnorm(0,.0001) }
}
sd ∼ dunif(0,5) # vague prior for between-trial standard deviation
var <- pow(sd,2) # between-trial variance
tau <- 1/var # between-trial precision
} # *** PROGRAM ENDS
Data
# High risk number transfused
# nt=no. treatments, ns=no. studies
list(nt=7,ns=56 )
r[,1] r[,2] n[,1] n[,2] t[,1] t[,2] na[]
31 21 41 40 1 4 2
7 4 31 30 1 4 2
21 17 29 30 1 4 2
8 7 25 25 1 4 2
1 2 33 32 1 3 2
30 19 30 30 1 3 2
3 1 24 23 1 3 2
19 6 49 41 1 3 2
64 41 102 98 1 5 2
10 8 15 15 1 5 2
13 9 50 52 4 6 2
27 20 60 60 4 6 2
19 9 26 24 4 6 2
12 5 20 20 4 6 2
73 57 103 99 4 6 2
13 12 29 24 2 6 2
14 13 50 50 5 7 2
33 31 111 102 2 7 2
27 20 38 38 1 2 2
5 6 17 20 1 2 2
51 51 96 97 1 2 2
10 8 43 44 1 2 2
23 15 50 50 1 2 2
7 2 25 22 1 2 2
41 24 165 147 1 2 2
12 7 20 20 1 2 2
8 5 33 33 1 2 2
21 15 40 40 1 2 2
8 7 39 40 1 2 2
12 7 31 29 1 2 2
221 166 278 274 1 2 2
54 42 59 58 1 2 2
27 8 50 50 1 2 2
6 3 30 32 1 2 2
54 37 115 116 1 2 2
8 3 40 36 1 2 2
17 0 108 106 1 2 2
63 35 140 143 1 2 2
9 7 14 15 1 2 2
4 2 20 20 1 2 2
8 9 14 16 1 2 2
12 15 20 41 1 2 2
37 29 40 42 1 2 2
4 3 20 20 1 2 2
13 14 19 19 1 2 2
27 28 44 42 1 2 2
16 12 44 37 1 2 2
10 7 31 62 1 2 2
27 11 106 104 1 2 2
9 2 14 16 1 2 2
18 12 24 24 1 2 2
11 13 15 15 1 2 2
43 22 75 75 1 2 2
22 15 50 50 1 2 2
74 60 100 100 1 2 2
108 98 177 189 1 4 2
END
INITS
# chain 1
list(sd=1, mu=c(2,0,3,0,2, -2,2,-2,-1,3, 2,-2,1,3,1, 1,2,-3,2,-2, -2,1,0,-3,3, 0,-3,-2,-3,-2, 3,-
3,0,-1,-3, 2,1,3,-2,2, 2,0,1,2,0, 0,-2,1,-2,-2, 2,1,1, 2,2,3),
d=structure(.Data=c(NA,0,1,0,0,-2,0, NA,NA,0,0,2,0,0, NA,NA,NA,0,0,0,0, NA,NA,NA,NA,0,0,0,
NA,NA,NA,NA,NA,0,0, NA,NA,NA,NA,NA,NA,0), .Dim = c(6,7)))
# chain 2
list(sd=1.5, mu=c(2,1,3,1,2, 0,2,0,-1,3, 2,0,1,3,1, 1,2,-3,2,0, 0,1,1,-3,3, 1,-3,0,-3,0, 3,-3,1,-1,-
3, 2,1,3,0,2, 2,1,1,2,1, 1,0,1,0,0, 2,3,1, -2,1,2),
d = structure(.Data =c(NA,0,1,0,0,-1,2, NA,NA,1,0.5,2,0,0, NA,NA,NA,2,1,1,0,
NA,NA,NA,NA,0.5,2,0,
NA,NA,NA,NA,NA,2,0, NA,NA,NA,NA,NA,NA,1 ), .Dim = c(6,7)))
# chain 3
list(sd=3, mu=c(2,0.5,3,0.5,2, -2,2,1,-1,3, 2,1,1,3,1, 1,2,-3,2,1, 1,1,0.5,-3,3, 0.5,-3,1,-3,1,
3,-3,0.5,-1,-3, 2,1,3,1,2, 2,0.5,1,2,0.5, 0.5,1,1,1,1, 2,1,0, -1,0,1),
d = structure(.Data =c(NA,0,1,0,0,-2,0, NA,NA,0,1,-2,0,-1, NA,NA,NA,2,0,1,0,
NA,NA,NA,NA,0,1,2,
NA,NA,NA,NA,NA,1,1, NA,NA,NA,NA,NA,NA,-1), .Dim = c(6,7)))
L.6.4. WinBUGS code for number of units of receiving allogeneic blood transfusions (High risk group)
UNITS TRANSFUSED - HIGH RISK
# Normal likelihood, identity link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
var[i,k] <- pow(se[i,k],2) # calculate variances
prec[i,k] <- 1/var[i,k] # set precisions
y[i,k] ∼ dnorm(theta[i,k],prec[i,k]) # binomial likelihood
theta[i,k] <- mu[i] + delta[i,k] # model for linear predictor
#Deviance contribution
dev[i,k] <- (y[i,k]-theta[i,k])*(y[i,k]-theta[i,k])*prec[i,k]
}
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(md[i,k],taud[i,k])
# mean of LOR distributions, with multi-arm trial correction
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k]
# precision of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k
# adjustment, multi-arm RCTs
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]])
# cumulative adjustment for multi-arm trials
sw[i,k] <- sum(w[i,1:k-1])/(k-1)
}
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for control arm
# vague priors for treatment effects
for (k in 2:nt){ d[k] ∼ dnorm(0,.0001) }
sd ∼ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# Provide estimates of treatment effects T[k] on the natural scale
# Given a Mean Effect, meanA, for 'standard' treatment A,
# with precision (1/variance) precA
A ∼ dnorm(meanA,precA)
for (k in 1:nt) { T[k] <- A + d[k] }
for (k in 1:nt) {
rk[k]<-rank(d[],k)
best[k]<-equals(rank(d[],k),1)}
for (c in 1:(nt-1))
{ for (k in (c+1):nt)
{ D[c,k] <- d[k] - d[c]}}
} # *** PROGRAM ENDS
Data
# ns= number of studies; nt=number of treatments
list(ns=23, nt=5, meanA=-1, precA=1)
t[,1] t[,2] y[,1] y[,2] se[,1] se[,2] na[]
1 2 11.17 6.47 1.263597349 1.121639956 2
1 2 1.38 0.53 0.207129187 0.102774024 2
1 2 2.4 1.54 0.258 0.22453656 2
1 2 0.7 0.4 0.2 0.16 2
1 4 2.22 1.2 0.073029674 0.04929503 2
2 5 1.68 0.87 0.453139052 0.196231156 2
2 5 3.21 1.58 0.107863874 0.100020831 2
1 3 0.87 0.41 0.109870053 0.077770507 2
1 3 1.57 0.8 0.400891863 0.278854801 2
1 3 1.7 0.8 0.402492236 0.171791138 2
1 3 7.75 5.33 0.996117463 0.890330329 2
1 3 0.76 0.92 0.241495342 0.188561808 2
1 3 3.03 1.42 0.82079623 0.347980348 2
1 3 3.13 2.87 0.852056336 0.490577891 2
1 3 9.16 4.1 2.694438717 0.910393688 2
1 3 12.4 7.9 2.529822128 1.043551628 2
1 3 1.68 0.52 0.2 0.18 2
1 3 1.4 0.8 0.194665705 0.129777137 2
1 3 3.17 2.03 0.092068326 0.074034324 2
1 3 6.51 3.93 0.439624185 0.281520895 2
1 3 9.36 4.84 1.485455474 0.768142632 2
1 3 1.62 0.91 0.239653736 0.147627794 2
1 3 1.65 1.25 0.053 0.055 2
END
Initial Values
#chain 1
list(d=c( NA, 0,0,0,0), sd=1, mu=c(0,0,0,0,0,0,0,0,0,0,0,1,1,1, 0, 0, 0, 0, 0, 1,1,1,0))
#chain 2
list(d=c( NA, -1,-3,1,-1), sd=4, mu=c(0,3,0,-1,0,2,1,0,-3,0,-2,1,1,1, 2, 0, 0, 1, 1,1,1,2,0))
#chain 3
list(d=c( NA, 2,2,2,2), sd=2, mu=c(2,3,1,-1,1,2,0,0,-3,0,2,1,-1,1,-2, 0, 0,-1,-1,1,1,-1,0))
L.6.5. WinBUGS code for length of stay in hospital (High risk group)
LENGTH OF STAY - HIGH RISK
# Normal likelihood, identity link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
var[i,k] <- pow(se[i,k],2) # calculate variances
prec[i,k] <- 1/var[i,k] # set precisions
y[i,k] ∼ dnorm(theta[i,k],prec[i,k]) # binomial likelihood
theta[i,k] <- mu[i] + delta[i,k] # model for linear predictor
#Deviance contribution
dev[i,k] <- (y[i,k]-theta[i,k])*(y[i,k]-theta[i,k])*prec[i,k]
}
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(md[i,k],taud[i,k])
# mean of LOR distributions, with multi-arm trial correction
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k]
# precision of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k
# adjustment, multi-arm RCTs
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]])
# cumulative adjustment for multi-arm trials
sw[i,k] <- sum(w[i,1:k-1])/(k-1)
}
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for control arm
# vague priors for treatment effects
for (k in 2:nt){ d[k] ∼ dnorm(0,.0001) }
sd ∼ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# Provide estimates of treatment effects T[k] on the natural scale
# Given a Mean Effect, meanA, for 'standard' treatment A,
# with precision (1/variance) precA
A ∼ dnorm(meanA,precA)
for (k in 1:nt) { T[k] <- A + d[k] }
for (k in 1:nt) {
rk[k]<-rank(d[],k)
best[k]<-equals(rank(d[],k),1)}
for (c in 1:(nt-1))
{ for (k in (c+1):nt)
{ D[c,k] <- d[k] - d[c]}}
} # *** PROGRAM ENDS
Data
# ns= number of studies; nt=number of treatments
list(ns=10, nt=6, meanA=-1, precA=1)
t[,1] t[,2] y[,1] y[,2] se[,1] se[,2] na[]
1 3 7.85 7.65 0.41900179 0.341525987 2
1 4 16.45 9.32 0.931428571 0.398243093 2
1 5 6.8 9.6 0.406138466 2.472393026 2
3 6 4 4.5 0.727590861 0.724640716 2
3 6 8.5 9.4 0.729143666 0.864332521 2
2 6 12.1 14.2 1.355575969 2.435279909 2
1 2 6.4 5.8 0.670820393 0.491934955 2
1 2 4.8 4.8 0.15666989 0.069631062 2
1 2 7.3 7.1 0.18973666 0.133333333 2
1 3 11.8 11.5 0.721580187 0.763762616 2
END
Initial Values
#chain 1
list(d=c( NA, 0,0,0,0,0), sd=1, mu=c(1,0, 0, 0, 0, 0, 1,1,0,2))
#chain 2
list(d=c( NA, -3,1,-1,-3,-1), sd=4, mu=c(1, 2, 0, 0, 1, 1,1,1,0,1))
#chain 3
list(d=c( NA, 2,2,2,2,2), sd=2, mu=c(-2, 1, 0, 0,-1,-1,1,1,0,1))
L.6.6. WinBUGS code for assessment of baseline risk of receiving allogeneic transfusions (Moderate risk group)
# Binomial likelihood, logit link
# Baseline random effects model
model{ # *** PROGRAM STARTS
for (i in 1:ns){ # LOOP THROUGH STUDIES
r[i] ∼ dbin(p[i],n[i]) # Likelihood
logit(p[i]) <- mu[i] # Log-odds of response
mu[i] ∼ dnorm(m,tau.m) # Random effects model
}
mu.new ∼ dnorm(m,tau.m) # predictive dist. (log-odds)
m ∼ dnorm(0,.0001) # vague prior for mean
var.m <- 1/tau.m # between-trial variance
tau.m <- pow(sd.m,-2) # between-trial precision = (1/between-trial variance)
sd.m ∼ dunif(0,5) # vague prior for between-trial SD
#tau.m ∼ dgamma(0.001,0.001)
#sd.m <- sqrt(var.m)
logit(R) <- m # posterior probability of response
logit(R.new) <- mu.new # predictive probability of response
}
Data
list(ns=69) # ns=number of studies
r[] n[]
16 20
23 70
9 102
15 19
8 21
13 34
10 17
10 22
10 30
12 52
17 82
15 80
24 30
13 86
12 190
11 56
54 658
4 62
12 42
24 43
15 19
8 20
8 25
2 6
7 10
3 12
12 13
34 38
13 21
13 21
26 26
13 78
1 20
10 50
102 120
45 50
6 20
55 100
15 38
14 25
4 51
4 5
14 24
7 330
7 20
1 50
23 53
1 16
11 32
6 90
20 73
20 34
8 19
10 20
8 20
3 14
10 37
18 88
7 25
8 24
10 45
20 35
47 50
12 36
18 45
9 35
12 20
19 40
11 49
END
Inits
list(mu=c( 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0,
0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,1,1), sd.m=1, m=0)
list(mu = c(1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1,
-1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-
1, -1,-1,2,1), sd.m=2, m= -1)
list(mu = c(1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1,
1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,0,0), sd.m = 0.5, m = 1)
L.6.7. WinBUGS code for number of adult patients receiving allogeneic transfusions (Moderate risk group)
NUMBER TRANSFUSED MODERATE RISK
# Binomial likelihood, logit link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ∼ dbin(p[i,k],n[i,k]) # binomial likelihood
logit(p[i,k]) <- mu[i] + delta[i,k] # model for linear predictor
rhat[i,k] <- p[i,k] * n[i,k] # expected value of the numerators
#Deviance contribution
dev[i,k] <- 2 * (r[i,k] * (log(r[i,k])-log(rhat[i,k]))
+ (n[i,k]-r[i,k]) * (log(n[i,k]-r[i,k]) - log(n[i,k]-rhat[i,k]))) }
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(md[i,k],taud[i,k])
# mean of LOR distributions (with multi-arm trial correction)
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k]
# precision of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k
# adjustment for multi-arm RCTs
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]])
# cumulative adjustment for multi-arm trials
sw[i,k] <- sum(w[i,1:k-1])/(k-1)
}
}
totresdev <- sum(resdev[]) # Total Residual Deviance
d[1]<-0 # treatment effect is zero for reference treatment
# vague priors for treatment effects
for (k in 2:nt){ d[k] ∼ dnorm(0,.0001) }
sd ∼ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# Provide estimates of treatment effects T[k] on the natural (probability) scale
# Given a Mean Effect, meanA, for 'standard' treatment A,
# with precision (1/variance) precA
A ∼ dnorm(meanA,precA)
for (k in 1:nt) { logit(T[k]) <- A + d[k] }
rr [1] < -1
for (k in 2:nt) {rr[k]<-T[k]/T[1] }
for (c in 1:(nt-1))
{ for (k in (c+1):nt)
{ lor[c,k] <- d[k] - d[c]
log(or[c,k]) <- lor[c,k]
lrr[c,k] <- log(rr[k]) - log(rr[c])
log(rrisk[c,k]) <- lrr[c,k] }}
for (k in 1:nt) {
rk[k]<-rank(rr[],k)
best[k]<-equals(rank(rr[],k),1)}
} # *** PROGRAM ENDS
Data
# ns= number of studies; nt=number of treatments
list(ns=73, nt=8, meanA=-0.5185, precA=0.479585024669854)
r[,1] r[,2] r[,3] n[,1] n[,2] n[,3] t[,1] t[,2] t[,3] na[]
16 10 NA 20 20 NA 1 4 NA 2
23 23 NA 70 70 NA 1 4 NA 2
9 8 NA 102 102 NA 1 4 NA 2
15 9 NA 19 17 NA 1 3 NA 2
8 1 NA 21 20 NA 1 3 NA 2
13 4 NA 34 26 NA 1 3 NA 2
10 3 NA 17 32 NA 1 3 NA 2
10 22 NA 22 47 NA 1 3 NA 2
10 5 NA 30 30 NA 1 3 NA 2
12 13 NA 52 52 NA 1 3 NA 2
17 6 NA 82 76 NA 1 3 NA 2
15 5 NA 80 80 NA 1 3 NA 2
24 4 NA 30 30 NA 1 3 NA 2
13 12 NA 86 92 NA 1 3 NA 2
12 29 NA 190 382 NA 1 3 NA 2
11 6 NA 56 59 NA 1 3 NA 2
54 33 23 658 321 321 1 3 5 3
4 2 NA 62 56 NA 1 5 NA 2
30 23 NA 74 73 NA 4 8 NA 2
6 1 NA 49 46 NA 3 7 NA 2
5 3 NA 49 49 NA 3 7 NA 2
13 9 NA 101 96 NA 2 6 NA 2
12 2 NA 42 41 NA 1 2 NA 2
24 8 NA 43 43 NA 1 2 NA 2
15 9 NA 19 20 NA 1 2 NA 2
8 4 NA 20 18 NA 1 2 NA 2
8 0 NA 25 25 NA 1 2 NA 2
2 0 NA 6 6 NA 1 2 NA 2
7 1 NA 10 10 NA 1 2 NA 2
3 0 NA 12 12 NA 1 2 NA 2
12 10 NA 13 15 NA 1 2 NA 2
34 17 NA 38 39 NA 1 2 NA 2
13 2 NA 21 21 NA 1 2 NA 2
13 2 NA 21 21 NA 1 2 NA 2
26 47 NA 26 73 NA 1 2 NA 2
13 1 NA 78 79 NA 1 2 NA 2
1 0 NA 20 26 NA 1 2 NA 2
10 15 NA 50 50 NA 1 2 NA 2
102 57 NA 120 120 NA 1 2 NA 2
45 28 NA 50 50 NA 1 2 NA 2
6 1 NA 20 20 NA 1 2 NA 2
55 34 NA 100 100 NA 1 2 NA 2
15 10 NA 38 38 NA 1 2 NA 2
14 16 NA 25 25 NA 1 2 NA 2
4 0 NA 51 50 NA 1 2 NA 2
4 1 NA 5 5 NA 1 2 NA 2
14 3 NA 24 27 NA 1 2 NA 2
7 2 NA 330 330 NA 1 2 NA 2
7 2 NA 20 20 NA 1 2 NA 2
1 0 NA 50 50 NA 1 2 NA 2
23 8 NA 53 47 NA 1 2 NA 2
1 0 NA 16 16 NA 1 2 NA 2
11 4 NA 32 32 NA 1 2 NA 2
6 1 NA 90 90 NA 1 2 NA 2
20 5 NA 73 73 NA 1 2 NA 2
20 9 NA 34 34 NA 1 2 NA 2
8 0 NA 19 20 NA 1 2 NA 2
10 13 NA 20 40 NA 1 2 NA 2
8 5 NA 20 19 NA 1 2 NA 2
3 1 NA 14 15 NA 1 2 NA 2
10 3 NA 37 36 NA 1 2 NA 2
18 7 NA 88 88 NA 1 2 NA 2
7 2 NA 25 25 NA 1 2 NA 2
8 1 NA 24 24 NA 1 2 NA 2
10 6 NA 45 90 NA 1 2 NA 2
20 12 NA 35 32 NA 1 2 NA 2
47 10 NA 50 50 NA 1 2 NA 2
12 3 NA 36 38 NA 1 2 NA 2
18 7 NA 45 45 NA 1 2 NA 2
9 5 NA 35 64 NA 1 2 NA 2
12 3 NA 20 20 NA 1 2 NA 2
19 10 NA 40 40 NA 1 2 NA 2
11 3 NA 49 52 NA 1 2 NA 2
END
Initial Values
list(
d=c(NA,0,0,0,0,0,0,0),
sd=.2,
mu=c(2,0,3,0,2, -2,2,-2,-1,3, 2,-2,1,3,1, 1,2,-3,2,-2, -2,1,0,-3,3, 0,-3,-2,-3,-2, 3,-3,0,-1,-3,
2,1,3,-2,2, 2,0,1,2,0, 0,-2,1,-2,-2, -3,1,-2,1,2, 2,0,1,2,0, 0,-1,2,0,-1, 1,1,1,1,1, 2,2,3))
list(
d=c(NA,1,1,1,1,1,1,1),
sd=.1,
mu=c(2,1,3,1,2, 0,2,0,-1,3, 2,0,1,3,1, 1,2,-3,2,0, 0,1,1,-3,3, 1,-3,0,-3,0, 3,-3,1,-1,-3,
2,1,3,0,2, 2,1,1,2,1, 1,0,1,0,0, -3,0,1,2,0, 2,0,3,0,2, -2,2,-2,-1,3, 2,0,3,0,2, -2,1,2))
list(
d=c(NA,0.5,0.5,0.5,0.5,0.5,0.5,0.5),
sd=.15,
mu=c(2,0.5,3,0.5,2, -2,2,1,-1,3, 2,1,1,3,1, 1,2,-3,2,1, 1,1,0.5,-3,3, 0.5,-3,1,-3,1, 3,-3,0.5,-1,-
3, 2,1,3,1,2, 2,0.5,1,2,0.5, 0.5,1,1,1,1, -3,-2,1,2, 0, 2,0,3,0,2, -2,2,-2,-1,3, 2,0,3,0,2, -1,0,1))
L.6.8. WinBUGS code for inconsistency model for number of adult patients receiving allogeneic transfusions (Moderate risk group)
Moderate risk number transfused
73 trials (including one 3-arm-trial),
8 treatments
# Binomial likelihood, logit link, inconsistency model
# Random effects model
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
delta[i,1]<-0 # treatment effect is zero in control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ∼ dbin(p[i,k],n[i,k]) # binomial likelihood
logit(p[i,k]) <- mu[i] + delta[i,k] # model for linear predictor
# Deviance contribution
rhat[i,k] <- p[i,k] * n[i,k] # expected value of the numerators
dev[i,k] <- 2 * (r[i,k] * (log(r[i,k])-log(rhat[i,k]))
+ (n[i,k]-r[i,k]) * (log(n[i,k]-r[i,k]) - log(n[i,k]-rhat[i,k])))
}
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(d[t[i,1],t[i,k]] ,tau)
}
}
totresdev <- sum(resdev[]) # Total Residual Deviance
for (c in 1:(nt-1)) { # priors for all mean treatment effects
for (k in (c+1):nt) { d[c,k] ∼ dnorm(0,.0001) }
}
sd ∼ dunif(0,5) # vague prior for between-trial standard deviation
var <- pow(sd,2) # between-trial variance
tau <- 1/var # between-trial precision
} # *** PROGRAM ENDS
Data
# Moderate risk number transfused
# nt=no. treatments, ns=no. studies
list(nt=8,ns=73 )
r[,1] r[,2] r[,3] n[,1] n[,2] n[,3] t[,1] t[,2] t[,3] na[]
16 10 NA 20 20 NA 1 4 NA 2
23 23 NA 70 70 NA 1 4 NA 2
9 8 NA 102 102 NA 1 4 NA 2
15 9 NA 19 17 NA 1 3 NA 2
8 1 NA 21 20 NA 1 3 NA 2
13 4 NA 34 26 NA 1 3 NA 2
10 3 NA 17 32 NA 1 3 NA 2
10 22 NA 22 47 NA 1 3 NA 2
10 5 NA 30 30 NA 1 3 NA 2
12 13 NA 52 52 NA 1 3 NA 2
17 6 NA 82 76 NA 1 3 NA 2
15 5 NA 80 80 NA 1 3 NA 2
24 4 NA 30 30 NA 1 3 NA 2
13 12 NA 86 92 NA 1 3 NA 2
12 29 NA 190 382 NA 1 3 NA 2
11 6 NA 56 59 NA 1 3 NA 2
54 33 23 658 321 321 1 3 5 3
4 2 NA 62 56 NA 1 5 NA 2
30 23 NA 74 73 NA 4 8 NA 2
6 1 NA 49 46 NA 3 7 NA 2
5 3 NA 49 49 NA 3 7 NA 2
13 9 NA 101 96 NA 2 6 NA 2
12 2 NA 42 41 NA 1 2 NA 2
24 8 NA 43 43 NA 1 2 NA 2
15 9 NA 19 20 NA 1 2 NA 2
8 4 NA 20 18 NA 1 2 NA 2
8 0 NA 25 25 NA 1 2 NA 2
2 0 NA 6 6 NA 1 2 NA 2
7 1 NA 10 10 NA 1 2 NA 2
3 0 NA 12 12 NA 1 2 NA 2
12 10 NA 13 15 NA 1 2 NA 2
34 17 NA 38 39 NA 1 2 NA 2
13 2 NA 21 21 NA 1 2 NA 2
13 2 NA 21 21 NA 1 2 NA 2
26 47 NA 26 73 NA 1 2 NA 2
13 1 NA 78 79 NA 1 2 NA 2
1 0 NA 20 26 NA 1 2 NA 2
10 15 NA 50 50 NA 1 2 NA 2
102 57 NA 120 120 NA 1 2 NA 2
45 28 NA 50 50 NA 1 2 NA 2
6 1 NA 20 20 NA 1 2 NA 2
55 34 NA 100 100 NA 1 2 NA 2
15 10 NA 38 38 NA 1 2 NA 2
14 16 NA 25 25 NA 1 2 NA 2
4 0 NA 51 50 NA 1 2 NA 2
4 1 NA 5 5 NA 1 2 NA 2
14 3 NA 24 27 NA 1 2 NA 2
7 2 NA 330 330 NA 1 2 NA 2
7 2 NA 20 20 NA 1 2 NA 2
1 0 NA 50 50 NA 1 2 NA 2
23 8 NA 53 47 NA 1 2 NA 2
1 0 NA 16 16 NA 1 2 NA 2
11 4 NA 32 32 NA 1 2 NA 2
6 1 NA 90 90 NA 1 2 NA 2
20 5 NA 73 73 NA 1 2 NA 2
20 9 NA 34 34 NA 1 2 NA 2
8 0 NA 19 20 NA 1 2 NA 2
10 13 NA 20 40 NA 1 2 NA 2
8 5 NA 20 19 NA 1 2 NA 2
3 1 NA 14 15 NA 1 2 NA 2
10 3 NA 37 36 NA 1 2 NA 2
18 7 NA 88 88 NA 1 2 NA 2
7 2 NA 25 25 NA 1 2 NA 2
8 1 NA 24 24 NA 1 2 NA 2
10 6 NA 45 90 NA 1 2 NA 2
20 12 NA 35 32 NA 1 2 NA 2
47 10 NA 50 50 NA 1 2 NA 2
12 3 NA 36 38 NA 1 2 NA 2
18 7 NA 45 45 NA 1 2 NA 2
9 5 NA 35 64 NA 1 2 NA 2
12 3 NA 20 20 NA 1 2 NA 2
19 10 NA 40 40 NA 1 2 NA 2
11 3 NA 49 52 NA 1 2 NA 2
END
INITS
# chain 1
list(sd=1, mu=c(2,0,3,0,2, -2,2,-2,-1,3, 2,-2,1,3,1, 1,2,-3,2,-2, -2,1,0,-3,3, 0,-3,-2,-3,-2, 3,-
3,0,-1,-3, 2,1,3,-2,2, 2,0,1,2,0, 0,-2,1,-2,-2, -3,1,-2,1,2, 2,0,1,2,0, 0,-1,2,0,-1, 1,1,1,1,1, 2,2,3),
d=structure(.Data=c(NA,0,1,0,0,-2,0,0, NA,NA,0,0,2,0,0,-2, NA,NA,NA,0,0,0,0,0,
NA,NA,NA,NA,0,0,0,0,
NA,NA,NA,NA,NA,0,0,1, NA,NA,NA,NA,NA,NA,0,0, NA,NA,NA,NA,NA,NA,NA,0), .Dim = c(7,8)))
# chain 2
list(sd=1.5, mu=c(2,1,3,1,2, 0,2,0,-1,3, 2,0,1,3,1, 1,2,-3,2,0, 0,1,1,-3,3, 1,-3,0,-3,0, 3,-3,1,-1,-
3, 2,1,3,0,2, 2,1,1,2,1, 1,0,1,0,0, -3,0,1,2,0, 2,0,3,0,2, -2,2,-2,-1,3, 2,0,3,0,2, -2,1,2),
d = structure(.Data =c(NA,0,1,0,0,-1,2,0, NA,NA,1,0.5,2,0,0,-2, NA,NA,NA,2,1,1,0,0,
NA,NA,NA,NA,0.5,2,0,1,
NA,NA,NA,NA,NA,2,0,1, NA,NA,NA,NA,NA,NA,1,0, NA,NA,NA,NA,NA,NA,NA,1), .Dim = c(7,8)))
# chain 3
list(sd=3, mu=c(2,0.5,3,0.5,2, -2,2,1,-1,3, 2,1,1,3,1, 1,2,-3,2,1, 1,1,0.5,-3,3, 0.5,-3,1,-3,1,
3,-3,0.5,-1,-3, 2,1,3,1,2, 2,0.5,1,2,0.5, 0.5,1,1,1,1, -3,-2,1,2, 0, 2,0,3,0,2, -2,2,-2,-1,3,
2,0,3,0,2, -1,0,1),
d = structure(.Data =c(NA,0,1,0,0,-2,0,0, NA,NA,0,1,-2,0,-1,0, NA,NA,NA,2,0,1,0,2,
NA,NA,NA,NA,0,1,2,0,
NA,NA,NA,NA,NA,1,1,1, NA,NA,NA,NA,NA,NA,-1,2, NA,NA,NA,NA,NA,NA,NA,2), .Dim =
c(7,8)))
L.6.9. WinBUGS code for number of units of receiving allogeneic blood transfusions (Moderate risk group)
Units Transfused - Moderate risk
# Normal likelihood, identity link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ∼ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
var[i,k] <- pow(se[i,k],2) # calculate variances
prec[i,k] <- 1/var[i,k] # set precisions
y[i,k] ∼ dnorm(theta[i,k],prec[i,k]) # binomial likelihood
theta[i,k] <- mu[i] + delta[i,k] # model for linear predictor
#Deviance contribution
dev[i,k] <- (y[i,k]-theta[i,k])*(y[i,k]-theta[i,k])*prec[i,k]
}
# summed residual deviance contribution for this trial
resdev[i] <- sum(dev[i,1:na[i]])
for (k in 2:na[i]) { # LOOP THROUGH ARMS
# trial-specific LOR distributions
delta[i,k] ∼ dnorm(md[i,k],taud[i,k])
# mean of LOR distributions, with multi-arm trial correction
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k]
# precision of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k
# adjustment, multi-arm RCTs
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]])
# cumulative adjustment for multi-arm trials
sw[i,k] <- sum(w[i,1:k-1])/(k-1)
}
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for control arm
# vague priors for treatment effects
for (k in 2:nt){ d[k] ∼ dnorm(0,.0001) }
sd ∼ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# Provide estimates of treatment effects T[k] on the natural scale
# Given a Mean Effect, meanA, for 'standard' treatment A,
# with precision (1/variance) precA
A ∼ dnorm(meanA,precA)
for (k in 1:nt) { T[k] <- A + d[k] }
for (k in 1:nt) {
rk[k]<-rank(d[],k)
best[k]<-equals(rank(d[],k),1)}
for (c in 1:(nt-1))
{ for (k in (c+1):nt)
{ D[c,k] <- d[k] - d[c]}}
} # *** PROGRAM ENDS
Data
# ns= number of studies; nt=number of treatments
list(ns=16, nt=4, meanA=-1, precA=1)
t[,1] t[,2] t[,3] y[,1] y[,2] y[,3] se[,1] se[,2] se[,3] na[]
1 3 NA 1.68 0.82 NA 0.330358657 0.259513119 NA 2
1 3 NA 0.71 0.05 NA 0.209489175 0.049193496 NA 2
1 3 NA 1.9 2.36 NA 0.221359436 0.189748638 NA 2
1 3 NA 1.06 0.54 NA 0.133789717 0.097375825 NA 2
1 3 NA 2.29 1.02 NA 0.305 0.28 NA 2
1 3 NA 1.74 0.22 NA 0.209960314 0.178922702 NA 2
1 3 4 2.68 1.26 3.49 0.122474487 0.121854359 0.104257207 3
1 2 NA 3.58 2.25 NA 0.453219961 0.275118156 NA 2
1 2 NA 3.46 2.29 NA 0.214373231 0.126118525 NA 2
1 2 NA 2.5 0.46 NA 0.538998189 0.316415941 NA 2
1 2 NA 1.6 1.8 NA 0.208710326 0.1394274 NA 2
1 2 NA 1.89 0.71 NA 0.12303658 0.110308658 NA 2
1 2 NA 1.55 0.55 NA 0.089461351 0.056597998 NA 2
1 2 NA 0.84 0.31 NA 0.159099026 0.113137085 NA 2
1 2 NA 1.11 0.76 NA 0.216898594 0.118585412 NA 2
1 2 NA 2.2 0.8 NA 0.223606798 0.178885438 NA 2
END
Initial Values
#chain 1
list(d=c( NA, 0,0,0), sd=1, mu=c(0,0,0,0,0, 0,0,0,0,0, 0,1,1,1, 0, 0))
#chain 2
list(d=c( NA, -1,-3,1), sd=4, mu=c(0,3,0,-1,0, 2,1,0,-3,0, -2,1,1,1, 2, 0))
#chain 3
list(d=c( NA, 2,2,2), sd=2, mu=c(2,3,1,-1,1, 2,0,0,-3,0, 2,1,-1,1,-2, 0))
L.6.10. WinBUGS code for assessment of baseline risk of mortality (High risk group)- for use in economic model
# Binomial likelihood, logit link
# Baseline random effects model
model{ # *** PROGRAM STARTS
for (i in 1:ns){ # LOOP THROUGH STUDIES
r[i] ∼ dbin(p[i],n[i]) # Likelihood
logit(p[i]) <- mu[i] # Log-odds of response
mu[i] ∼ dnorm(m,tau.m) # Random effects model
}
mu.new ∼ dnorm(m,tau.m) # predictive dist. (log-odds)
m ∼ dnorm(0,.0001) # vague prior for mean
var.m <- 1/tau.m # between-trial variance
tau.m <- pow(sd.m,-2) # between-trial precision = (1/between-trial variance)
sd.m ∼ dunif(0,5) # vague prior for between-trial SD
#tau.m ∼ dgamma(0.001,0.001)
#sd.m <- sqrt(var.m)
logit(R) <- m # posterior probability of response
logit(R.new) <- mu.new # predictive probability of response
}
Data
list(ns=24) # ns=number of studies
r[] n[]
1 41
15 23
1 40
2 29
0 25
3 97
4 50
0 23
3 96
1 165
2 31
3 278
1 59
3 150
3 20
1 14
4 40
4 19
0 16
0 31
2 106
2 45
2 75
5 177
END
Inits
list(mu=c( 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0), sd.m=1, m=0)
list(mu = c(1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1,-1, -1,-1,-1,-1), sd.m=2, m= -1)
list(mu = c(1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1), sd.m = 0.5, m = 1)
L.6.11. WinBUGS code for assessment of baseline risk of mortality (Moderate risk group)-for use in economic model
# Binomial likelihood, logit link
# Baseline random effects model
model{ # *** PROGRAM STARTS
for (i in 1:ns){ # LOOP THROUGH STUDIES
r[i] ∼ dbin(p[i],n[i]) # Likelihood
logit(p[i]) <- mu[i] # Log-odds of response
mu[i] ∼ dnorm(m,tau.m) # Random effects model
}
mu.new ∼ dnorm(m,tau.m) # predictive dist. (log-odds)
m ∼ dnorm(0,.0001) # vague prior for mean
var.m <- 1/tau.m # between-trial variance
tau.m <- pow(sd.m,-2) # between-trial precision = (1/between-trial variance)
sd.m ∼ dunif(0,5) # vague prior for between-trial SD
#tau.m ∼ dgamma(0.001,0.001)
#sd.m <- sqrt(var.m)
logit(R) <- m # posterior probability of response
logit(R.new) <- mu.new # predictive probability of response
}
Data
list(ns=10) # ns=number of studies
r[] n[]
0 62
1 38
0 78
0 100
0 42
1 35
0 50
0 35
0 86
0 57
END
Inits
list(mu=c( 0,0,0,0,0, 0,0,0,0,0), sd.m=1, m=0)
list(mu = c(1,-1,-1,-1,-1, -1,-1,-1,-1,-1), sd.m=2, m= -1)
list(mu = c(1,1,1,1,1, 1,1,1,1,1), sd.m = 0.5, m = 1)
- Network meta-analysis of alternatives to blood transfusion in surgical patients ...Network meta-analysis of alternatives to blood transfusion in surgical patients - Blood Transfusion
Your browsing activity is empty.
Activity recording is turned off.
See more...
