Selection of the case study

The decision to offer oral bisphosphonates for the primary prevention of osteoporotic fragility fracture is a second potentially illuminating case study for examining the impact of competing risks and DTD on CEAs. The risk factors for fragility fracture include many behavioural (e.g. smoking) and pathological (e.g. type 1 diabetes) factors that are also associated with shorter life expectancy. Failing to account for these factors could lead to inflated estimates of the value of medicines that reduce the risk of fracture. Furthermore, although there is little doubt that oral bisphosphonates are effective in reducing incidence of fragility fracture, bisphosphonates are inconvenient to take, and this raises the possibility that DTD may attenuate or even outweigh the gains that previous CEAs have estimated.

NICE initially recommended two oral bisphosphonates (i.e. alendronic acid and risedronate sodium) in in its Technology Appraisal 160 in 2008.¹⁴⁶ A subsequent appraisal (i.e. TA464¹²) confirmed this decision and added a third oral medicine in the class (i.e. ibandronic acid) to the recommended options. The evidence available to the decision-making committee for TA464¹² included a CEA, synthesising evidence on the benefits, harms and costs of preventative treatments, including oral bisphosphonates. The analysis concluded that oral bisphosphonates are likely to represent an effective use of NHS resources for anyone whose 10-year risk of MOF exceeds 1.5%.¹⁴⁷

The same authors updated their model as part of a further health technology assessment (HTA) for a subsequent NICE appraisal, and this focused on antiosteoporosis medicines other than bisphosphonates, but included bisphosphonates as comparators, although NICE subsequently chose to suspend the appraisal.¹⁴⁸ The updated model found that a somewhat higher level of risk, than in TA464,¹² would be necessary for oral bisphosphonates to provide reasonable value for money, although the precise threshold is not quantified.¹⁴⁹

The model underpinning these analyses was a discrete-event simulation. Unlike the cohort model explored in Chapter 6, discrete-event simulations work by generating a virtual population of people and simulating their lives one by one. Discrete-event simulations handle competing events by randomly generating next-event times for all outcomes of interest, processing the event that will occur first and then, depending on event type and model structure, moving on to the next event or recalculating some or all next-event times to reflect the simulated person’s updated history. The simulation may also terminate (e.g. if the event is death).

Given adequate data and implementation, discrete-event simulation is an appropriate way of accounting for competing events and, because the model handles them simultaneously, it is appropriate to parameterise each event distribution using time-to-event methods that censor for competing events. This is because, in a patient-level simulation as in clinical reality, events compete naturally, and the occurrence of some events will preclude the occurrence of others. In the case in hand, some simulated people will experience hip fracture before death; however, some people will experience death first, thereby precluding a fracture event (although the model ‘knows’ when that person was destined to experience a fracture had death not intervened).

Therefore, in contrast to the situation where we want to estimate the probability that a single event in isolation will occur (as in the epidemiological analyses in Chapters 2 and 3), modellers developing simulations with multiple events need inputs for each that censor for intervening events. In the case in hand, we actively want our estimates of time to hip fracture to reflect a world in which death is not possible (e.g. relying on a Kaplan–Meier estimator censoring for death), as the model will simultaneously and independently apply an estimate of time to death. So long as both inputs represent valid estimates for the modelled population, the incidence of hip fracture observed in the model will replicate the Aalen–Johansen estimator in a real population.

However, as with a cohort model, if the estimate for any one of our competing events is biased, then we will have biased results for all outcomes. Again, a commonly overlooked question is whether or not unadjusted general population lifetables represent an appropriate estimate of life expectancy for the people the model simulates. In a patient-level model, we have information about some characteristics for each person simulated. It is common to use the age and sex of the simuland to inform the distribution from which the model draws the time to all-cause death. However, other characteristics may also be associated with greater or lesser life expectancy. In the case in hand, we are particularly interested in predicted fracture risk. If people with high fracture risk also have an increased risk of other-cause death and we fail to account for this, then we will overestimate the number of fractures that occur and this, in turn, will overstate the clinical effectiveness and cost-effectiveness of any intervention that has the potential to reduce fracture incidence.

Previous models have estimated that the benefits of bisphosphonates for the average person are, in absolute terms, small. TA464¹² found that, when compared with no treatment, alendronate is associated with an average health gain no greater than 0.00247 QALYs, even in the highest-risk tenth of people.¹² The 2020 HTA¹⁴⁹ introduced a little more benefit for oral bisphosphonates, but alendronate still conferred only mean gains in the range of 0.0001–0.0058 QALYs (equivalent to up to 2 quality-adjusted days of life in perfect health), depending on baseline risk.

These small benefits should not be casually dismissed, given the low cost of the intervention and the large population who could expect, on average, to gain. Nevertheless, it is clear that it would not take much to offset the expected gains. Both TA464¹² and the 2020 HTA¹⁴⁹ incorporate an estimate of QALY loss owing to adverse gastrointestinal effects for a proportion of people taking oral alendronate. However, these analyses do not reflect the fact that, even when well tolerated, oral bisphosphonates are inconvenient to take. As we have seen (see Chapter 5), even when taken weekly, oral bisphosphonates are associated with non-trivial DTD (significantly greater than for daily statins). Therefore, it is plausible that the routine downsides of taking bisphosphonates might attenuate or outweigh their benefits in preventing fractures, although this trade-off has not previously been explored.

Our aim was to explore the impact that better accounting for competing risk of death and incorporation of DTD might have on the estimated cost-effectiveness of bisphosphonates. TA464¹² stipulates that prescribers should offer bisphosphonate treatment ‘when [it] is appropriate, taking into account [the person’s] risk of fracture, their risk of adverse effects from bisphosphonates, and their clinical circumstances and preferences’ (© NICE 2017 Bisphosphonates for Treating Osteoporosis. Available from www.nice.org.uk/guidance/ta464. All rights reserved. Subject to Notice of rights). Although fracture risk and adverse events are central to previous analyses of the cost-effectiveness of bisphosphonates, there has been little formal consideration of how decision-making might be affected by people’s clinical circumstances and preferences. The methods introduced in this project enable us to explore these dimensions and weigh them against the benefits and harms that existing models estimate.

Model overview

The model is a patient-level discrete-event simulation. Figure 21 illustrates the structure of the model and Table 19 summarises key design criteria. Where state-transition models define a healthcare pathway in terms of states, discrete-event models proceed by way of events. The events that are possible in the TA464 model¹² are fractures (divided into four categories of hip, vertebral, proximal humerus and wrist), admission to full-time care and death (fracture related and other cause). Simulated people who experience fractures incur costs and disutility, and their risk of additional negative events (e.g. further fractures, admission to full-time care, death) increases.

FIGURE 21

Structure of discrete-event model: events that can occur in a simulated person’s lifetime.

Our study focused exclusively on the pairwise comparison between oral alendronate and no treatment. Our DTD elicitation exercise did not distinguish between different oral bisphosphonates, and alendronate is, by some distance, the most commonly prescribed chemical in the class, consistently accounting for over 80% of prescriptions of agents classified in British National Formulary section 6.6 (drugs affecting bone metabolism).¹⁵¹

General model updates

We performed fewer general updates to the bisphosphonates model than we did for the statins analysis. Producing a revised best estimate of the cost-effectiveness of bisphosphonates is beyond the scope of this project and analysis, therefore, focuses on exploring whether or not accounting for competing risks and DTD would have materially affected the historical analyses. One exception is that we have updated how the model implements persistence with oral therapy (see below), as this not only influences the effectiveness of bisphosphonates but also has potentially important implications for DTD, which is one of our central concerns.

The 2020 bisphosphonates HTA¹⁴⁹ introduced some other modifications to the TA464 model¹² that we have adopted as detailed below.

New model features specific to this project

Accounting for competing risk of non-fracture death

To estimate non-fracture death in people at risk of osteoporotic fragility fracture, we used identical methods to those we adopted for non-cardiovascular death in people at risk of CVD (see Chapter 6, Accounting for competing risk of non-cardiovascular death).

First, we fitted a model to estimate average population fracture risk as a function of age and sex (see Appendix 9, Table 57 and Figure 61). We noted that, in the CPRD data set, a relatively consistent exponential increase in risk throughout the first nine decades of life tails off somewhat in people in their nineties. We found it necessary to use a seventh-order polynomial term to capture this shape adequately. This feature is contrary to expectation, as there is no mathematical characteristic of the QFracture-2012 model that would lead to a waning of hazard.²⁶ Therefore, we think it is likely that selection effects in the underlying data set led to over-representation of nonagenarians with QFracture-2012 estimates that are low relative to expectation. To explore the impact of this issue, we fitted an alternative model on a restricted data set that comprised only people younger than 90 years, allowing the model to project the observed trend from people aged 30–89 years for people in their nineties, and in this case a quartic function sufficed (see Appendix 9, Table 57 and Figure 61).

As for the non-cardiovascular death model in Chapter 6, we fitted a relative survival model to estimate the multiplicative difference in time to non-fracture death between a person in the CPRD extract and someone of the same age and sex in the general population. Again, our critical covariate is Δlogit(Q), that is the difference (on a log-odds scale) between each individual’s predicted 10-year QFracture-2012 risk of major fracture and the average score for a person of the same age and sex, as estimated in the models described above.

We fitted a simple, univariable model with Δlogit(Q) as the only covariate and a more complex one with Δlogit(Q), age, polynomial terms for both and interactions between them, as per Equation 1. We tried models with Δlogit(Q) defined using each of the QFracture-2012 prediction models in Appendix 9, Table 57, and found that the relative survival model fitted better (with meaningfully lower AIC) when we used the model fitted on only people younger than 90 years. Therefore, this was the version of the relative survival model we took forward.

Table 20 shows outputs of the relative survival models for men and women.

TABLE 20

Relative survival models: non-fracture mortality as a function of predicted fracture risk and age in men and women

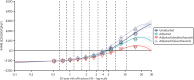
Figure 22 shows estimates of non-fracture mortality generated in the way described above, compared with empirical data across different categories of cardiovascular risk and age. The empirical Kaplan–Meier curves represent observed non-fracture mortality (censored for fracture death) in the CPRD extract for people of the stated age, with baseline QFracture-2012 predictions in the specified brackets (see Figure 22). For our modelled estimates, we start from ONS 3-year lifetables for England and Wales (we use 2009–11 tables, as this is in the middle of the period covered by the CPRD data). We adjust the data to remove fracture deaths, estimated using proportions recorded under ICD-10 code M80 in the ONS’s ‘Deaths registered in England and Wales’ series. For each combination of risk and age bracket, we calculate HRs, as described above (for comparability, we fit at the mean QFracture-2012 prediction and age observed within that category in the CPRD data), and apply the HRs to the ONS curves, and this produces the adjusted curves shown in Figure 22.

FIGURE 22

Fitted relative survival model for non-fracture mortality compared with empirical data. (a) Men; and (b) women.

The fitted models provide a less strikingly accurate fit to the observed data than we saw with non-cardiovascular mortality, but still represent a substantial improvement over the unadjusted estimates. Larger coefficients are estimated for the polynomial terms in the more complex model, meaning that it diverges from the simple model to a somewhat greater extent than we saw for non-cardiovascular mortality.

Some instances in which the fitted models appear to depart from the empirical data seem to be due to incoherencies in the observed curves. For instance, it appears that women aged 60–69 years with a 10-year risk of less than 1% and women a decade older with a 1–2% risk have worse survival than the models predict. However, if this is true, then it means that women at this low risk have worse survival than women with higher fracture risk, which is both hard to explain and inconsistent with the patterns seen elsewhere in the data, where increasing risk is invariably associated with worse survival.

We incorporated the relative survival models into the health economic decision model by calculating a fitted HR for each sampled patient and applying it when calculating their life expectancy.

Deriving results

For TA464, the modellers presented results from a single model run comprising 2 million virtual people (c. 200,000 per risk-stratified tenth), with parameter uncertainty propagated at the individual level (i.e. the model samples new parameter values from distributions reflecting uncertainty in their true value for each patient). Our preliminary investigation suggested that there is still non-trivial Monte Carlo error in the model with that many runs, but this generally appears to stabilise after around 4 million patients. Therefore, our base-case results summarise the outputs of 5 million people (c. 500,000 per tenth).

To enable us to explore results further, as in TA464, we fitted a generalised additive model (GAM) to the patient-level outputs of the discrete-event model. The response variable is incremental net monetary benefit for alendronate compared with no treatment. In its simplest version, the meta-model takes the form:

where g(.) is a link function (i.e. identity, as we assume a Gaussian distribution for INMB), f(.) is a smooth term (with a cubic regression spline basis function) that can capture non-linearities in the relationship between the predictor (i.e. baseline QFracture-2012 10-year serious fracture probability) and the response term, and Adj is a dummy variable indicating whether or not the economic model was adjusted for competing risk of non-fracture death.

We also extended the meta-modelling methods used in TA464 to provide an estimate of value for money as a function of baseline risk and age. This model takes the form:

Here, the joint effect of fracture risk and age becomes the target of the smooth term. As before, we stratify the model by adjustment condition.

As in previous iterations of the model,^149,150 we found that GAM predictions become erratic above a predicted 10-year fracture risk of 30%, owing to the very small numbers of simulated patients who reach this level of risk (i.e. around 0.1% of the cohort). Therefore, we fitted the meta-model to a data set excluding the few simulated people who exceed this level of risk and present only fitted results up to this threshold.

Accounting for competing risk

Table 21 summarises expected events with alendronate compared with no treatment, first in the unadjusted model and then in the version that adjusts for competing risk of non-fracture death. Table 21 presents analogous information to Table 9 in the 2020 HTA.¹⁴⁹ Table 37 of the analysis underpinning TA464¹⁵⁰ has something similar, although note that this is based on an uncorrected network meta-analysis, and the corrigendum does not include an updated version of the same information.¹⁴⁷

TABLE 21

Modelled effectiveness of alendronate: clinical outcomes

Whether adjusted for competing risk or not, the updated model estimates that alendronate prevents slightly more fractures than the previous models in all categories except wrist fracture, and this is because the longer duration of treatment (and consequent extension of offset period) gives more time for the intervention to provide benefit. The reduced efficacy for wrist fracture compared with the 2020 HTA¹⁴⁹ is probably a result of different inputs, for example the network meta-analysis developed for the 2020 HTA¹⁴⁹ included a wider range of comparators and estimated a greater mean effect for bisphosphonates in preventing wrist fractures.

Comparing adjusted with unadjusted models reveals some relatively subtle differences. In higher-risk people (most obviously in the highest-risk tenth), the unadjusted model slightly overstates the effectiveness of alendronate. We can see this when we take account of the fact that people with high risk of fracture also experience increased risk of competing causes of death, with the result that fewer of people live to see the benefit of future fractures prevented. With a large enough sample, we would also expect to see the unadjusted model underpredicting fractures in the people with below-average risk (because their true life expectancy is longer than the unadjusted model simulates). There may be a hint of this type of effect in the lowest-risk tenth of the population; however, we would need a colossal sample size to detect the effect reliably, as events are so rare (and intervening deaths even rarer) in the few years during which the treatment effect obtains.

Table 22 shows how these dynamics translate into costs and QALYs. In absolute terms, the adjusted model generates more QALYs than the unadjusted model for people at lowest risk of fracture, and the relationship reverses as risk rises. Comparing incremental results from the unadjusted and adjusted models shows no difference in the deciles in which oral bisphosphonates represent an effective use of NHS resources. In both versions of the model, the lower-risk seven-tenths of people gain a tiny benefit from alendronate, but this benefit is insufficient to offset the additional costs associated with the intervention. Above the seventh decile, however, QALY gains get a bit larger and (because fractures cause expense to the health and care system, as well as disutility to the person) incremental costs go down, with the result that preventative treatment provides reasonable value for money (when we value QALYs at £20,000 each). In the adjusted model, the degree of net benefit expected for people at highest risk is discernibly lower than in the unadjusted version, and this is a direct result of the smaller number of fractures prevented, as discussed above. Nevertheless, both models agree about the people for whom incremental net benefit is positive.

TABLE 22

Cost-effectiveness results for alendronate compared with no treatment: effect of adjusting for competing risk of non-fracture death

Figure 23 shows the output of the GAM meta-model (see Equation 4) fitted to patient-level output and it is directly analogous to the green line in Figure 3 in the corrigendum to the analysis that informed TA464¹⁴⁷ (with the difference that we find it helpful to show the x-axis on a logarithmic scale; note that the first seven deciles of risk all fit into the first sixth of the natural scale graph). This is consistent with what we have seen in previous model outputs, that is the unadjusted model overestimates benefit in people at greatest risk as, once we adjust for competing risk of other-cause death, their capacity to benefit from reduced fracture risk diminishes.

FIGURE 23

Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of risk of fracture, with different assumptions about competing risk of non-fracture death. GAM fitted to model outputs comprising 5 million (more...)

However, as seen before, the levels of risk at which this bias operates are almost exclusively above the point where – both adjusted and unadjusted models agree that – intervention provides positive net benefit. The unadjusted model suggests that the threshold at which alendronate becomes cost-effective is a 10-year MOF risk of 4.7 (95% CI 4.5 to 4.9), whereas the adjusted model estimates the same value as 5.0 (95% CI 4.8 to 5.2).

Extending the GAM meta-model to incorporate age as well as baseline risk (see Equation 5) produces outputs such as those illustrated in Figure 24 (fitted at indicative ages of 50, 60, 70 and 80 years). By and large, results replicate those in the unstratified meta-model, that is we may overestimate value for money in people at the highest risk if we do not adjust for competing risk of non-fracture death; however, this generally only affects the magnitude of expected benefit in people for whom some degree of benefit is expected. There is some indication that these expectations may diverge for the youngest people. For example, for 50-year-olds, treatment is only cost-effective in the highest-risk tenth of people once we adjust for competing risk. Note, however, that the outputs of the meta-model are much more uncertain, in this instance, as they are based on a far smaller sample size (almost all simulated people with the highest level of fracture risk are aged > 50 years).

FIGURE 24

Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of age and risk of fracture, with different assumptions about competing risk of non-fracture death. (a) Age 50 years; (b) age 60 years; (c) (more...)

Appendix 9, Table 58, shows the threshold at which treatment becomes associated with positive net benefit according to the GAM, adjusting for age and fracture risk. Unadjusted model outputs are relatively invariant to age, whereas the adjusted model suggests that the threshold for intervention should fall as people get older (until they reach the oldest category).

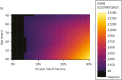
As we did with the statins model, we also looked at how it would affect cost-effectiveness results if we simulated people who are fitter or less fit than average (over and above the degree that would be expected via fracture risk alone), by halving and doubling each individual’s HR for non-fracture death. Figure 25 shows results for model 2, which adjusts for fracture risk only. Figure 26 shows the same for model 2 but adjusts for age as well. Figure 27 shows a cross-categorisation of age and fracture risk, with varying assumptions about competing risk. As would be expected, we can see that the threshold at which intervention generates positive incremental net benefit is somewhat higher in people who are more likely to die of other things and somewhat lower in people whose increased life expectancy gives them every chance of surviving to realise the benefit of fractures prevented.

FIGURE 25

Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of risk of fracture, with different assumptions about competing risk of non-fracture death. GAM fitted to model outputs comprising 5 million (more...)

FIGURE 26

Cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment) as a function of age and risk of fracture, with different assumptions about competing risk of non-fracture death. (a) Age 50 years; (b) age 60 years; (c) (more...)

FIGURE 27

Relationship between age, risk of fracture and cost-effectiveness of bisphosphonates (incremental net monetary benefit compared with no treatment), with different assumptions about competing risk of non-fracture death. (a) Unadjusted (as per TA464); (b) (more...)

Incorporating direct treatment disutility

We show the lifetime discounted QALY losses we would expect from DTD in Table 23. Permanent and time-limited losses are identical because, in our base case, we assume that time-limited DTD lasts for 10 years and alendronate therapy is capped at 5 years. Therefore, under both scenarios, people experience full DTD for as long as they take the drug.

TABLE 23

Lifetime discounted QALY loss arising from DTD under various assumptions about duration of effect

To give context to our estimates of DTD, we should remember that, as shown in Table 22, once we adjust for competing risk of non-fracture death, expected QALY gains associated with alendronate compared with no treatment are small (with no more than 0.005 QALYs per person), even in people at the highest risk of fracture. Even under the assumption of diminishing DTD, we estimate that people stand to lose more than 10 times as many QALYs from DTD as they stand to gain from the fracture-preventing effect of alendronate. Any version of Figure 27 that also accounted for any degree of DTD would comprise exclusively black area, as there is no combination of patient characteristics that leads to expected QALY gains that come close to justifying estimated DTD.

In the competing risk-adjusted model, fewer than 0.2% of simulated people experience QALY gains that are greater than their expected DTD (in permanent, time-limited and diminishing DTD scenarios). Even in the 10% of people at highest risk of fracture, these percentages rise to only 0.53–0.58%, depending on DTD scenario, and this suggests that if DTD is present then at least 199 out of 200 people treated with bisphosphonates would experience more harm than benefit, even if their chances of fracture are high.

Even if we assume that people get used to taking bisphosphonates over a short period of 1 year, QALY losses associated with DTD are still at least five times greater than expected QALY gains. The conclusion is inescapable: for anybody experiencing any duration of DTD of the magnitude estimated in Chapter 5, it is impossible to anticipate long-term benefits that would offset the up-front harm.

Main findings

Although we would reiterate that our results should not be seen as a present-day best estimate of the cost-effectiveness of bisphosphonates, our results are closely comparable with the results generated in previous iterations of the same underlying model.^147,149,150 Alendronate is associated with small but positive net benefit in people with approximately the highest-third of fracture risk (i.e. anything above around 5% per year).

As with the cohort-level model explored in Chapter 6, ‘adjusting for competing risk’ in a discrete event simulation does not mean introducing a new concept that has, hitherto, been absent from such analyses. Rather, ‘adjusting for competing risk’ means taking the competing time-to-event functions the model has always simulated and ensuring that we parameterise the functions in a way that accounts for important correlations between them. We find that ‘adjusting for competing risk’ has a relatively subtle effect on model outputs, as it makes a small difference to the magnitude of expected benefit, but the people for whom adjustment makes the greatest absolute difference are people for whom adjusted and unadjusted models predict at least some degree of benefit. This is consistent with findings in our analysis of risk prediction models that miscalibration is often most obvious in people whose level of risk clearly exceeds intervention thresholds (see Chapters 2–4).

In contrast, the effects of DTD in the same decision space are anything but subtle. At the level at which we measured the effects of DTD for bisphosphonates (see Chapter 5), DTD of any duration would be enough to swamp expected benefit from fracture prevention. The low rates of persistence with oral bisphosphonates observed in practice are further evidence that people associate bisphosphonates with disutility of a magnitude that outweighs any anticipated gain, which lends some face validity to our findings. It follows that, once we factor cost into the equation, it is impossible to find any identifiable group of people for whom oral bisphosphonates represent an effective use of NHS resources if we assume population-level average DTD for everyone to whom the decision applies. In fact, there are a small number of simulated people for whom bisphosphonates would be cost-effective at conventional QALY values despite these people experiencing net harm (as this can occur when non-trivial cost savings arise from prevented fractures and associated QALY gains are marginally less than DTD-related QALY losses).

Nevertheless, in the same way we argued for statins for the primary prevention of CVD (see Chapter 6, Discussion), we would not suggest that decision-makers should advocate blanket disinvestment in bisphosphonates. On the one hand, we think it is useful information that the average person would sacrifice more quality-adjusted life expectation to avoid taking bisphosphonates than they could expect to gain from their therapeutic effect (and this is true both of people with experience of taking bisphosphonates and members of the general public). On the other hand, although our survey respondents were more eager to avoid bisphosphonates than statins, around one-sixth of the respondents still ascribed no DTD to bisphosphonates. Therefore, if adequately informed people consider the trade-off differently to the average person (and they are at sufficiently high risk of fragility fracture to justify the costs of treatment), then we would still want to offer people access to a treatment from which they could expect some benefit before any counterweighting from disadvantages they are prepared to tolerate.

Limitations

First, our epidemiological work (see Chapter 3) finds that QFracture-2012 is poorly calibrated for reasons not limited to its inability to deal with competing risks, and, on the face of it, this would seem to undermine our cost-effectiveness model that, in common with its previous iterations, predicts risk of fracture using baseline QFracture-2012 predictions. However, in the world simulated by our decision-analytic model, QFracture-2012 does not have poor predictive utility but, instead, has perfect predictive utility because the model simulates events as a direct function of each simulated person’s baseline risk (i.e. the simulated people in the model really do have the risk of fracture that QFracture-2012 would ascribe to them). Therefore, our results can be seen as assessing the cost-effectiveness of bisphosphonates in a population with accurate risk prediction. This means that our results would be valid for the more accurate risk estimates that a better risk prediction model would produce. The only areas in which QFracture-2012’s poor calibration may undermine the model are (1) the deciles of risk by which the population is subdivided bear little relation to the true risks faced in the population and (2) for TA464, the modellers derived the distributional assumptions underpinning time-to-fracture events from analysis of QFracture-2012 data (see ‘Estimating time to event from absolute fracture risk’ in Davis et al.¹⁵⁰). If a more accurate risk prediction model implied different functional forms and/or shape parameters, then this ought to be reflected in an updated cost-effectiveness model.

Second, as with our relative survival model for non-cardiovascular death, we acknowledge that collapsing risk to a single covariate (in this case, 10-year major fracture risk) runs the risk of lumping together people with different non-fracture survival expectations. For example, a 70-year-old woman with no long-term conditions but a family history of osteoporosis has an identical QFracture-2012 prediction to a 70-year-old woman with type 2 diabetes and CKD but no family history (as both have a 12.6% chance of major fragility fracture over 10 years). It is plausible that, although their risk of fracture is indistinguishable, these two profiles would be associated with markedly different life expectancy. Our relative survival model is blind to such dynamics, as the model uses fracture risk as a single covariate. When comparing our adjusted life expectancy estimates with observed data (see Figure 22), we acknowledge that, for some age–sex–fracture risk strata, there are larger discrepancies between modelled and observed outcomes than we saw with the cardiovascular data set. We might be able to achieve a closer fit with a more sophisticated model (i.e. instead of using a summary risk prediction measure we could estimate relative survival as a function of each of the individual covariates on which the prediction itself relies). Such an approach would theoretically be able to capture the differential effect of risk factors for fracture on life expectancy. However, this would be a very complex model to fit, and we could only validate it against ever-more stratified subsections of the empirical data, which, even when starting from a large data set, would swiftly lead to sample-size constraints. At very least, we remain confident that our simpler modelling approach results in much better estimates of life expectancy than relying on unadjusted general population data, as has been done in all previous models.

Third, our results suggest that, after one accounts for competing risk of non-fracture death, the risk threshold for intervention with bisphosphonates goes down as people get older. This is the opposite of what is recommended in NICE Quality Standard 149 (QS149),¹⁶⁴ where intervention thresholds rise with age. The thresholds in QS149¹⁶⁴ derive from an analysis by McCloskey et al.,¹⁶⁵ the predominant aim of which was to reduce the number of people in whom treatment is indicated. Our modelling suggests that a younger person with higher risk of fracture has less capacity to benefit because they are likely to be substantially less healthy than an average person of the same age and sex, with the consequence that their life expectancy leaves less room for fracture prevention. An older person with the same estimated risk will not stand out from their contemporaries in the same way and so their life expectancy will be closer to typical.

Fourth, the modelled population has a lower proportion of people with a high fracture risk than the real population because the simulation does not account for correlations between risk factors. For example, when the model generates a simuland with type 2 diabetes, then that person is no more likely than an average member of the population to have CKD or CVD, whereas, in reality, such risk factors cluster together. This has the effect that there are unrepresentatively few people with multiple risk factors and, hence, higher fracture risk in the simulated data set. This issue may have caused or compounded the problems we encountered fitting meta-models to full data sets, leading us to truncate the data to people with predicted 10-year fracture risks lower than 30% (see Deriving results).

Finally, given the computational demands of producing a probabilistic sensitivity analysis, this was not possible for this study.

Conclusion

Similar to the analysis presented in Chapter 6, this analysis has shown that including competing risk in the model-based CEA of bisphosphonates for primary prevention produced only subtle changes to the observed cost-effectiveness. However, we noted some effect and this analysis provides more evidence that competing risk should be included in CEAs of primary prevention strategies. Incorporating DTD had a dramatic effect on the cost-effectiveness of bisphosphonates. The effect was so dramatic that the observed QALY gains from taking a bisphosphonate were swamped by DTD in all scenarios. This result raises an interesting challenge to decision-makers in the context of bisphosphonates. However, rather than advise bisphosphonates should not be recommended because of the possible DTD, we advise that the impact of including DTD in sensitivity analyses on the outputs of a decision-analytic model should be an integral component of CEAs of primary prevention strategies.